Примеры решения задач. Пример 1. От двух когерентных источников S1 и S2 (l = 0.8 мкм) лучи попадают на экран

Пример 1. От двух когерентных источников S₁ и S₂ (l = 0.8 мкм) лучи попадают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную пленку (n = 1.33), интерференционная картина изменилась на противоположную. При какой наименьшей толщине d_min пленки это возможно?

Решение. Изменение интерференционной картины на противоположную означает, что на тех участках экрана, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционной картины возможен при изменении оптической разности хода пучков световых волн на нечетное число половин длин волн, т.е.

D₂ - D₁ = (2k+1)l/2, (1)

где D₁ - оптическая разность хода пучков световых волн до внесения пленки;

D₂ - оптическая разность хода тех же пучков после внесения пленки;

k = 0, +1, +2, ...,+k_max.

Наименьшей толщине d_min пленки соответствует k = 0. При этом формула (1) примет вид

D₂ - D₁ = l/2. (2)

Выразим оптические разности хода D₂ и D₁:

D₁ = l₁ - l₂, D₂ = [(l₁ - d_min)+n×d_min] - l₂ = (l₁-l₂) + d_min(n-1). Подставим выражения D₁ и D₂ в формулу (2):

(l₁-l₂) + d_min(n-1) - (l₁-l₂) = l/2.

или

d_min(n-1) = l/2.

Отсюда

d_min = l/[2(n-1)].

Произведем вычисления:

= 1,21 мкм.

Пример 2. Определить импульс p и кинетическую энергию T электрона, движущегося со скоростью v = 0,9 c, где c - скорость света в вакууме.

Решение. Импульсом частицы называется произведение массы частицы на её скорость:

p = mv. (1)

Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле

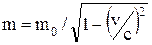, (2)

где m - масса движущейся частицы; m_o - масса покоящейся частицы;

b = v/c - скорость частицы, выраженная в долях скорости света.

Заменив в формуле (1) массу m её выражением (2) и приняв во внимание, что v = cb, получим выражение для релятивистского импульса:

. (3)

Произведём вычисления:

p = 9,31×10^-31×0,9×3×10³/ =5,6×10^-23 кг×м/с.

В релятивистской механике кинетическая энергия T частицы определяется как разность между полной энергией и энергией покоя E_o этой частицы, т.е.

T = E - E_o. Так как E = mc² и E_o = m_oc², то учитывая зависимость массы от скорости, получаем:

. (4)

Произведём вычисления:

.

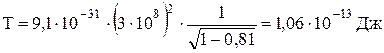Пример 3. Длина волны, на которую приходится максимум энергии в спектре излучения черного тела, l_max = 0,58 мкм. Определить энергетическую светимость R_e поверхности тела.

Решение. Энергетическая светимость R_e абсолютно чёрного тела в соответствии с законом Стефана - Больцмана пропорциональна четвёртой степени термодинамической температуры и выражается формулой

R_e = sT⁴, (1)

где s- постоянная Стефана - Больцмана; T -абсолютная температура.

Температуру T - можно вычислить с помощью закона смещения Вина:

l_o = b/T, (2)

где b - постоянная закона смещения Вина.

Используя формулы (2) и (1), получаем

R_e = s(b/l)⁴. (3)

Произведём вычисления:

R_e = 5,67×10^-8×(2,9×10^-3/5,8×10^-7)⁴ = 3,54×10⁷ Вт/м².

Пример 4. Определить максимальную скорость v_max фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны l₁ = 0,155 мкм; 2) g - излучением с длиной волны l₂ = 1 пм.

Решение. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для внешнего фотоэффекта:

e = A + T_max, (1)

где e - энергия фотонов, падающих на поверхность металла; A - работа выхода; T_max - максимальная кинетическая энергия фотоэлектронов.

Энергию фотона можно вычислить по формуле:

e= hc/l, (2)

где h - постоянная Планка; c - скорость света в вакууме; l - длина волны.

Кинетическая энергия электрона может быть выражена или по классической формуле

T = m_ov²/2, (3)

или по релятивистской формуле

, (4)

в зависимости от того, какая скорость сообщается фотоэлектрону. Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект; если энергия e фотона много меньше энергии покоя E_o электрона, то может быть применена формула (3), если же e сравнима с E_o, то вычисление по формуле (3) приводит к ошибке, поэтому нужно пользоваться формулой (4).

1. Вычислим энергию фотона ультрафиолетового излучения по формуле (2):

e₁ = 6,63×10^-34×3×10⁸/1,55×10^-7 = 1,28×10^-18 Дж

или

e₁ = 1,28×10^-18/1,6×10^-19 = 8 эВ.

Полученная энергия фотона e₁ < E_o (E_o = 0,51 МэВ - энергия покоя электрона). Следовательно, в данном случае кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3):

e₁ = A + m_ov²_max/2.

откуда

. (5)

Подставив значения величин в формулу (5), найдём

v_max= .

Вычислим энергию фотона g - излучения:

e₂ = hc/l = 6,63×10^-34×3×10⁸/1×10¹² = 1,99×10^-13 Дж,

или во внесистемных единицах

e₂ = 1,99×10^-13/1,6×10^-19 = 1,24×10⁶ эВ = 1,24 МэВ.

Работа выхода электрона (A = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (e₂ = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона: T_max = 1,24 МэВ. Так как в данном случае кинетическая энергия электрона больше его энергии покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии (4). Из этой формулы найдём

.

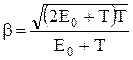Заметив, что v = cb и T_max = e₂, получим

.

Произведём вычисления:

.

Пример 5. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол q = 90^o. Энергия рассеянного фотона e₂ = 0,4 МэВ. Определить энергию фотона e₁ до рассеяния.

Решение. Для определения энергии первичного фотона воспользуемся формулой Комптона:

, (1)

где Dl = l₂ - l₁ - изменение длины волны фотона в результате рассеяния на свободном электроне; h - постоянная Планка; m_o – масса покоя электрона; c - скорость света в вакууме; q- угол рассеяния фотона.

Преобразуем формулу (1):

1) заменим в ней Dl на l₂ - l₁;

2) выразим длины волн l₁ и l₂ через энергии e₁ и e₂ соответствующих фотонов, воспользовавшись формулой e = hc/l;

3) умножим числитель и знаменатель правой части формулы на c, тогда

Сократим на hc и выразим из этой формулы искомую энергию:

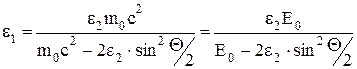(2)

где E_o = m_oc² - энергия покоя электрона.

Вычисления по формуле (2) удобнее вести во внесистемных единицах. Так как для электрона E_o = 0,511 МэВ, то

e₁ = 0,4×0,511/(0,511 - 2×0,4×sin²45^o) = 1,85 МэВ.

Пример 6. Пучок монохроматического света с длиной волны l = 663 нм падает на зеркальную плоскую поверхность. Поток излучения Ф_e = 0,6 Вт. Определить 1) силу давления F, испытываемую этой поверхностью; 2) число фотонов ежесекундно падающих на поверхность.

Решение. 1. Сила светового давления на поверхность равна произведению светового давления p на площадь S поверхности:

F = pS. (1)

Световое давление может быть найдено по формуле:

p = E_e(r + 1)/c, (2)

где E_e - энергетическая освещённость поверхности; c - скорость света в вакууме; r - коэффициент отражения.

Подставляя правую часть выражения (2) в формулу (1), получаем

F = E_eS(r + 1)/с. (3)

Так как E_eS представляет собой поток излучения Ф_e, то

F = Ф_e(r + 1)/c. (4)

Произведём вычисления, учитывая, что для зеркальной поверхности r=1:

F = 0,6(1 + 1)/3×10⁸ = 4 нН.

2. Произведение энергии e одного фотона на число фотонов n₁, ежесекундно падающих на поверхность, равно мощности излучения, т.е. потоку излучения: Ф_e = e×n₁, а так как энергия фотона e == hc/l, то

Ф_e = h×c×n₁l, откуда

n₁ = Фel/(hc). (5)

Произведём вычисления:

n₁ = 0,6×6,63×10^-7/(6,63×10^-34×3×10⁸) = 2×10¹⁸ с^-1.