Примеры решения задач. Пример 1. Электрон в атоме водорода перешел с четвёртого энергетического уровня на второй

Пример 1. Электрон в атоме водорода перешел с четвёртого энергетического уровня на второй. Определить энергию испущенного при этом фотона.

Решение. Для определения энергии фотона воспользуемся сериальной формулой Бальмера для водородоподобных ионов:

. (1)

где l - длина волны фотона; R - постоянная Ридберга; Z - заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода); n₁ - номер орбиты, с которой перешел электрон; n₂ - номер орбиты, на которую перешел электрон ( n₁ и n₂ - главные квантовые числа).

Энергия фотона e выражается формулой

e = h×c/l

Поэтому, умножив обе части равенства (1) на hc, получим выражение для энергии фотона:

.

Так как Rhc есть энергия ионизации E_i атома водорода, то

.

Вычисления выполним во внесистемных единицах:

E_i = 13,6 эВ. Z = 1; n₁ = 2; n₂ = 4:

e = 13,6×1²(1/2² - 1/4²) эВ = 13,6×3/16 = 2,55 эВ.

Пример 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля электрона для двух случаев: 1) U₁ = 51 В; 2) U₂ = 510 кВ.

Решение. Длина волны де Бройля для частицы зависит от её импульса p и определяется формулой

l_Б = h/p, (1)

где h - постоянная Планка.

Импульс частицы можно определить, если известна её кинетическая энергия T. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше её энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).

В нерелятивистском случае

,

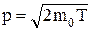где m_o - масса покоя электрона.

В релятивистском случае

. (3)

где E_o = m_oc² - энергия покоя электрона.

Формула (1) с учётом соотношений (2) и (3) запишется: в нерелятивистском случае

, (4)

в релятивистском случае

. (5)

Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U₁ = 51 В и U₂ = 510 кВ, с энергией покоя электрона и в зависимости от этого решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля.

Электрическое поле совершает над электроном работу, которая равна изменению его кинетической энергии T:

T = e×U

В первом случае T₁ = e×U = 51 эВ = 0,51×10^-4 МэВ, что много меньше энергии покоя электрона E_o = m_oc² = 0,51 МэВ. Следовательно, в этом случае можно применить формулу (4). Для упрощения расчётов заметим, что T₁ = =10^-4m_oc². Подставив это выражение в формулу (4), перепишем её в виде

.

Учитывая, что h/m_oc есть комптоновская длина волны L, получим

l₁ = 10²L× .

Так как L = 2,43 пм, то

l₁ = 10²×2,43/ = 171 (пм).

Во втором случае кинетическая энергия T₂ = eU₂ = 510 кэВ = 0,51МэВ, т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Так как T₂ = m_oc², то по формуле (5) находим

.

Подставим значение L и произведём вычисления:

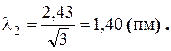
Пример 3. Кинетическая энергия электрона в атоме водорода составляет величину порядка T = 10 эВ. Используя соотношение неопределённостей, оценить минимальные линейные размеры атома.

Решение. Соотношение неопределённостей для координаты и импульса имеет вид

Dx×Dp_x ³ ћ, (1)

где Dx - неопределённость координаты x электрона; Dp_x - неопределённость проекции импульса электрона на ось X; ħ - постоянная Планка, делённая на 2p.

Из соотношения неопределённостей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределённым становится соответствующая проекция импульса, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределённостью

Dx = l/2.

Соотношение неопределённостей (1) можно записать в том случае в виде

(l/2)Dp_x ³ ħ,

откуда

l ³ 2ħ/Dp_x. (2)

Физически разумная неопределённость импульса Dp_x во всяком случае не должна превышать значения самого импульса p_x, то есть Dp_x £ p_x. Импульс p_x связан с кинетической энергией T соотношением p_x = (2mT)^1/2. Переходя от неравенства к равенству, получим

. (3)

Произведём вычисления:

l_min = 2×1,05×10^-34/(2×9,1×10^-31×1,6×10^-19×10)^1/2 = 124 нм.

Пример 4. Волновая функция описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность нахождения частицы в малом интервале Dl = 0,01l в двух случаях: 1) вблизи стенки (0 < x < l);

2) в средней части ящика ((l - Dl)/2 ≤ x ≤(l + Dl)/2).

Решение. Вероятность того, что частица будет обнаружена в интервале dx (от x до x + dx), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние, равна

dw = êy(x)ê²×dx.

В первом случае искомая вероятность найдётся интегрированием в пределах от 0 до 0,01l:

.

Так как x изменяется в интервале 0 ≤x ≤0,01l и, следовательно, px/l <l, справедливо приближённое равенство

sin²(px/l) » (px/l)².

С учётом этого выражение (1) примет вид

.

После интегрирования получим

w = .

Во втором случае можно обойтись без интегрирования, так как квадрат модуля волновой функции вблизи её максимума в заданном малом интервале (Dl = =0,01l) практически не изменяется. Искомая вероятность во втором случае определяется выражением

w = 2×(sin²(pl/2l)×Dl/l = 2×0,01l/l = 0,02.

Пример 5. Найти заряд ядра атомов вещества, для которых K_a-линия в характеристическом рентгеновском спектре имеет длину волны l=193,5 пм.

Решение. По закону Мозли 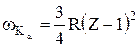, где Z - зарядовое число ядра атома, R = 2,067×10¹⁶ с^-1 Отсюда выразим Z

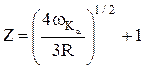, w=2pn= 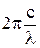, откуда

Ответ: Q=+26e.

Пример 6. На медную фольгу, у которой n×d = 1,5×10^-2 кг/м², падает перпендикулярно узкий пучок a - частиц, энергия которых 5,29 МэВ. На угол q > 6° рассеивается больше 1% всех a-частиц. Определить число протонов Z в ядре меди.

Решение. Рассеяние a-частиц на ядрах атомов описывается формулой Резерфорда:

По условию задачи a частицы рассеиваются в пределах углов 6°<q <180°, поэтому число рассеянных a-частиц можно определить интегрированием:

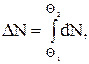т.е. (1)

По условию задачи DN/N ³ 0,01. Выполнив в (1) некоторые преобразования, получим

. (2)

Для определения Z необходимо найти nd - число ядер фольги на единицу ее поверхности. В условии задачи дается rd, поэтому nd находим по формуле:

,

где m = 0,064 кг/моль, N_А - число Авогадро.

Количество протонов в ядре меди найдём из уравнения (2):

, 4pctg²3⁰=4573

Ответ: Z = 29.

Пример 7. Узкий пучок протонов с кинетической энергией Т = 100 кэВ падает перпендикулярно на золотую фольгу, для которой rd = 10² кг/м². Протоны под углом q=60° регистрирует счетчик с круглым отверстием S=1 см², которое расположено на расстоянии R = 10 см от участка фольги, рассеивающей протоны. Отверстие счетчика расположено перпендикулярно к направлению падающих на него протонов. Доля рассеянных протонов, падающих на отверстие счетчика, составляет DN/N = 4×10^-4. Определить массовое число ядра атома золота.

Решение. Для нахождения массового числа А примем, что М_ат » А×m_N.и воспользуемся формулой :

. (1)

В условии задачи задана площадь S, на которую под углом q в пределах Dq падают частицы. Поскольку площадка и количество частиц DN имеют определенные значения, уравнение (1) необходимо записать в интегральной форме:

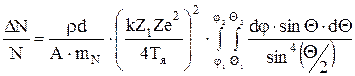. (2)

Учитывая малые изменения углов q и j интеграл в выражении (2) запишем в следующем виде:

(3)

где q - среднее значение угла q.

Используя приближение (3), определим А:

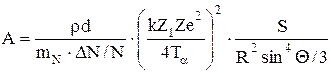. (4)

Ответ: А = 194.

Пример 8. Вычислить сечение ядра атома золота, которое соответствует рассеянию протонов с кинетической энергией Т = МэВ в пределах углов q от 60° до 180°.

Решение. Рассеяние частиц ядром в пределах углов от q до q + dq определяется площадью ds эффективного сечения ядра в виде кольца (рис.1.1):

ds = 2pbdb . (1)

Прицельное расстояние b найдем из формулы:

, (2)

где q₁ - заряд протона, q₂ - заряд ядра золота. Дифференциал от b равен:

; (3)

Подставив выражение (2) и (3) в (1), получим:

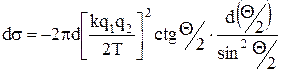; (4)

Сечение ядра, на котором рассеиваются частицы в пределах углов от q₁ до q₂:

. (5)

Подставим выражение (4) в интеграл (5):

. (6)

После интегрирования получим:

,

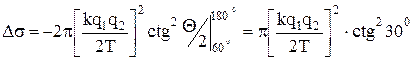где q₁=+e, q₂=78e.

: Ds= 2,1-10^-26 м².

Пример 9. Атомное ядро, поглотив g - фотон (l = 0,47 пм), возбудилось, после чего распалось на отдельные нуклоны, которые разлетелись в разных направлениях. Суммарная кинетическая энергия нуклонов равна 0,4 МэВ. Определить энергию связи Е_св ядра.

Решение. На основании закона сохранения энергии имеем:

М_я + hn = Zm_p + (А - Z)m_n + Т,

где Т - кинетическая энергия нуклонов. Энергия связи:

E_св = Z×m_p + (A-Z)m_n – M_я = hn - T.

E_св=hn - T = hc/l - T.

Произведём вычисления

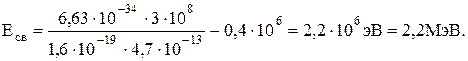
Ответ: Е_св = 2,2 МэВ.

Пример 10. Рассчитать с помощью формулы Вейцзеккера энергию связи Са⁴⁰.

Решение. Полуэмпирическая формула Вейцзеккера позволяет найти энергию связи ядра по его значениям А и Z:

E_св=14A - 13A^2/3 - 0,584Z²/A^1/3 - 19,3 .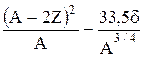

Для ядра Ca⁴⁰ d = -1.

E_св = 14×40 - 13×40^2/3 - 0,58×20²/40^2/3 – 19,3(40-40)/20 - 33,5×(-1)/40^3/4 = 342 МэВ.

Ответ: Е. = 342 МэВ.

Пример 11. а) Определить с помощью формулы Вейцзеккера заряд Z ядра, которое имеет наименьшую массу среди ядер с одинаковым нечетным значением массового числа А.

б)Определить с помощью полученной формулы характер активности следующих b активных ядер: Ag¹⁰³ и Sn¹²⁷.

Решение. а) Воспользовавшись формулой Вейцзеккера, выразим массу ядра как функцию А и Z:

M_я = Z×m_p + (A-Z)m_n – 14A + 13A^2/3 0,584×Z²/A^1/3 +19,3× .

При заданном А масса ядра является функцией Z, т.е. М_я = f(Z) (рис.1.2). Чтобы найти Z_min, найдём производную dM/dZ и приравняем её к нулю:

dM(Z)/dZ = 0.

Функция М(Z) имеет один минимум.

Решив уравнение dM(Z)/dZ = 0 относительно Z, получим ответ на вопрос задачи:

dM/dZ=m_p-m_n + 2Z×0,584/A^1/3 +19,3× = 0.

m_p-m_n=1,007276-1,008665=1,3 МэВ, 78,5=Z(154,4/A+1,17A^-1/3).

Z_min=78,5A/154,4+1,17A^2/3=A/1,98+0,015A^2/3.

б) Определим Z_min для А = 103, .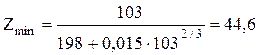

Но Z может быть только целым числом, поэтому принимаем Z_min = 45. Радиоактивность Аg¹⁰³ будет направлена на уменьшение Z, поэтому распад ядра идет по схеме:

.

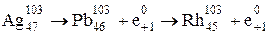Находим Z_min для А = 127:

Z_min=54.

Распад ядра ведет к увеличению Z. Из этого следует, что оно обладает электронной активностью:

.

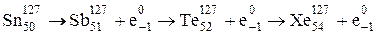Ответ: Z_min = А/(1,98 + 0,015 А^2/3).

Пример 12. Вычислить дефект массы и энергию связи ядра .

Решение. Масса ядра всегда меньше суммы масс свободных (находящихся на очень больших расстояниях друг от друга ) протонов и нейтронов, из которых состоит ядро. Дефект массы ядра Dm равен разности между суммой масс свободных нуклонов и массой ядра, т.е.

Dm = Zm_p + (A - Z)m_n - m_я, (1)

где Z - порядковый номер (число протонов в ядре); m_p, m_n, m_я - соответственно массы протона , нейтрона и ядра.

В справочных таблицах всегда даются массы нейтральных атомов, а не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в неё входила масса m_a нейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку ядра: m_a = m_я + Zm_e, откуда

m_я = m_a - m_e. (2)

Выразив в равенстве (1) массу ядра по формуле (2), получаем

Dm = Z(m_p + m_e) + (A - Z)m_n - m_a.

Замечая, что m_p+m_e=m_H, где m_H- масса атома водорода, находим

Dm = Zm_H + (A - Z)m_n - m_a. (3)

Подставив в выражение (3) числовые значения масс, взятые из справочной таблицы, получим

Dm = [3×1,00783 + (7 - 3)×1,00867 - 7×0,1601] = 0,04216 (а.е.м.)

В соответствии с законом пропорциональности массы и энергии

E = Dm×c², (4)

где c - скорость света в вакууме.

Коэффициент пропорциональности c² можно выразить через массу и энергию: c² = E/Dm = 9×10¹⁶ Дж/кг.

Если вычислять энергию связи, используя внесистемные единицы, то c² = 931,44 МэВ/а.е.м. С учётом этого формула (4) примет вид

E = 93,44×Dm (МэВ). (5)

Подставив значение дефекта массы ядра в формулу (5), получим

E = 931,44×0,04216 МэВ = 39,2 МэВ.

Пример 13. Вычислить толщину слоя половинного ослабления X_1/2 параллельного пучка g - излучения для воды, если линейный коэффициент ослабления m = 0,047 см^-1.

Решение. Интенсивность g - излучения в зависимости от толщины слоя убывает по закону:

I = I_oexp(-mx). (1)

Пройдя поглощающий слой половинного ослабления пучок будет иметь интенсивность I = I_o/2. Подставив значения I и x в формулу (1), получим I_o/2 = I_oexp(-m×x_1/2), или после сокращения:

1/2 = exp(-mX_1/2). (2)

Прологарифмировав последнее выражение, получим искомое значение толщины слоя половинного ослабления:

X_1/2 = ln(2)/m. (3)

Произведём вычисления

X_1/2 = ln(2)/4,7 = 14,7 см.

Пример 14. Кремниевый образец нагревают от температуры t₁ = 0^oC до температуры t₂ = 10^oC. Во сколько раз возрастает его удельная проводимость?

Решение. Удельная проводимость g собственных полупроводников связана с температурой T соотношением

g = g₀×exp(-DE/(2kT)),

где g₀ - константа; DE - ширина запрещённой зоны. Следовательно,

.

Полагая для кремния DE = 1,1 эВ, произведём вычисления:

.