Волновые свойства частиц

Длина волны де Бройля

l = h/p,

где p - импульс частицы.

Импульс частицы и его связь с кинетической энергией Т:

а) p = m_ov; 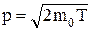, при v << c;

б) ; при v » c,

где m_o - масса покоя частицы;

m - релятивистcкая масса;

v - скорость частицы;

c - скорость света в вакууме;

E_o - энергия покоя частицы (E_o = m₀c²).

Соотношения неопределенностей:

а) Dp_x×Dx ³ ћ (для координаты и импульса),

где Dp_x - неопределенность проекции импульса частицы на ось Х;

Dx - неопределенность координаты x частицы;

б) DE×Dt .³ ћ (для энергии и времени),

где DE - неопределенность энергии;

Dt - время жизни квантовой системы в данном энергетическом состоянии.

Одномерное уравнение Шредингера для стационарных состояний:

,

где y(x) - волновая функция, описывающая состояние частицы;

m - масса частицы;

E - полная энергия;

U = U(x) -потенциальная энергия частицы.

Плотность вероятности

,

где dw(x) - вероятность того, что частица может быть обнаружена вблизи точки с координатой x на участке dx.

Вероятность обнаружения частицы в интервале от x₁ до x_2:

.

Решение уравнения Шрёдингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:

а) ;

б) ,

где y_n(x) - собственная нормированная волновая функция;

E_n - собственное значение энергии микрочастицы;

n - квантовое число (n= = 1, 2, 3, ...);

l - ширина ящика.

Вероятность проникновения частицы через одномерный высокий прямоугольный потенциальный барьер конечной ширины:

,

где l - ширина барьера;

ћ - постоянная Планка, делённая на 2p;

m - масса микрочастицы;

U - высота потенциального барьера;

E - энергия микрочастицы.