МЕХАНИКА

основные формулы

КИНЕМАТИКА

• Положение материальной точки в пространстве задается радиусом-вектором:

где — единичные векторы направлений (орты); — координаты точки.

Кинематические уравнения движения в координатной форме:

где t — время.

• Средняя скорость:

.

где — перемещение материальной точки за интервал времени .

• Средняя путевая скорость:

где 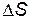— путь, пройденный точкой за интервал времени .

• Мгновенная скорость:

где — проекции скорости на оси координат.

Модуль скорости:

.

• Ускорение:

,

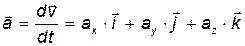где: - проекции ускорения на оси координат.

Модуль ускорения: .

При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих:

.

Модули этих ускорений:

; ; ,

где R — радиус кривизны в данной точке траектории.

• Кинематическое уравнение равномерного движения материальной точки вдоль оси х:

,

где — начальная координата; t — время. При равномерном движении

и .

• Кинематическое уравнение равнопеременного движения ( ) вдоль оси x:

,

где v₀ ‑ начальная скорость; t ‑ время.

Скорость точки при равнопеременном движении:

.

• Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) .

Кинематическое уравнение вращательного движения:

.

• Средняя угловая скорость:

,

где — изменение угла поворота за интервал времени . Мгновенная угловая скорость:

.

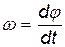• Угловое ускорение:

.

• Кинематическое уравнение равномерного вращения:

,

где - начальное угловое перемещение; t - время. При равномерном вращении и .

Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения.

• Частота вращения:

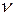=N/t, или 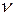=1/T,

где N — число оборотов, совершаемых телом за время t; Т — период вращения (время одного полного оборота).

• Кинематическое уравнение равнопеременного вращения ( .)

,

где - начальная угловая скорость; t - время.

Угловая скорость тела при равнопеременном вращении

.

• Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:

путь, пройденный точкой по дуге окружности радиусом R,

( - угол поворота тела);

скорость точки линейная

; ;

ускорение точки:

тангенциальное

; ;

нормальное

; .

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ТЕЛА, ДВИЖУЩИХСЯ ПОСТУПАТЕЛЬНО

• Уравнение движения материальной точки (второй закон Ньютона):

в векторной форме:

, или ,

где — геометрическая сумма сил, действующих на материальную точку; т — масса; — ускорение;— импульс; N — число сил, действующих на точку;

в координатной форме (скалярной):

, ,

или

, , ,

где под знаком суммы стоят проекции сил , на соответствующие оси координат.

Сила гравитационного взаимодействия:

,

где G — гравитационная постоянная; m₁ и m₂ — массы взаимодействующих тел, рассматриваемые как материальные точки; r — расстояние между ними.

Сила трения скольжения:

,

где 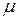— коэффициент трения скольжения; N — сила нормального давления.

• Сила упругости:

,

где k — коэффициент упругости (жесткость в случае пружины);

— абсолютная деформация.

• Координаты центра масс системы материальных точек:

, , ,

где m_i — масса i-й материальной точки; x_i, y_i;, z_i; — ее координаты.

• Закон сохранения импульса:

или ,

где N — число материальных точек (или тел), входящих в систему.

• Работа, совершаемая постоянной силой:

или ,

где 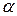— угол между направлениями векторов силы и перемещения .

• Работа, совершаемая переменной силой:

,

где интегрирование ведется вдоль траектории, обозначаемой L.

• Средняя мощность за интервал времени :

.

• Мгновенная мощность:

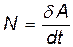или ,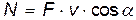

где — работа, совершаемая за промежуток времени dt.

• Кинетическая энергия материальной точки (или тела), движущейся поступательно:

или .

• Потенциальная энергия тела и сила, действующая на тело в данной точке поля, связаны соотношением

или ,

где— единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (как, например, гравитационное),

.

• Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины)

.

• Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами m₁, и т₂, находящихся на расстоянии r друг от друга:

.

• Потенциальная энергия тела, находящегося в однородном поле силы тяжести,

=mgh,

где h — высота тела над уровнем, принятым за нулевой для отсчета потенциальной энергии. Эта формула справедлива при условии , где R — радиус Земли.

• Закон сохранения энергии в механике выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде:

+ =const.

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ

• Момент силы , действующей на тело, относительно оси вращения:

,

• Момент инерции относительно оси вращения:

а) материальной точки

,

где т — масса точки; r — расстояние ее от оси вращения;

б) дискретного твердого тела

,

где — масса i-го элемента тела; r_i — расстояние этого элемента от оси вращения; N — число элементов тела;

в) сплошного твердого тела

.

Если тело однородно, т. е. его плотность 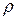одинакова по всему объему, то

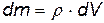и ,

где V — объем тела.

• Моменты инерции некоторых тел правильной геометрической формы:

Тело	Ось, относительно которой определяется момент инерции	Формула момента инерции
Однородный тонкий стержень массой т и длиной l	Проходит через центр тяжести стержня перпендикулярно стержню
Проходит через конец стержня перпендикулярно стержню
Тонкое кольцо, обруч, труба радиусом R и массой т, маховик радиусом R и массой т, распределенной по ободу	Проходит через центр перпендикулярно плоскости основания
Круглый однородный диск (цилиндр) радиусом R и массой т	Проходит через центр диска перпендикулярно плоскости основания
Однородный шар массой т и радиусом R	Проходит через центр шара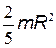

• Теорема Штейнера. Момент инерции тела относительно произвольной оси:

,

где J₀ — момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; а — расстояние между осями; m — масса тела.

• Момент импульса вращающегося тела относительно оси:

.

• Закон сохранения момента импульса:

,

где L_i — момент импульса i-го тела, входящего в состав системы. Закон сохранения момента импульса для двух взаимодействующих тел:

где — моменты инерции и угловые скорости тел до взаимодействия: — те же величины после взаимодействия.

Закон сохранения момента импульса для одного тела, момент инерции которого меняется:

,

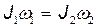где 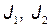— начальный и конечный моменты инерции; — начальная и конечная угловые скорости тела.

• Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:

,

где 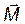— момент силы, действующей на тело в течение времени dt;

J — момент инерции тела;— угловая скорость; — момент импульса.

В случае постоянного момента инерции основное уравнение динамики вращательного движения принимает вид

,

где — угловое ускорение.

• Работа постоянного момента силы М, действующего на вращающееся тело:

A=Mj ,

где j — угол поворота тела.

• Мгновенная мощность, развиваемая при вращении тела,

.

• Кинетическая энергия вращающегося тела

.

• Кинетическая энергия тела, катящегося по плоскости без скольжения:

,

где — кинетическая энергия поступательного движения тела; v — скорость центра инерции тела; 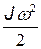,— кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции.

РЕЛЯТИВИСТСКАЯ МЕХАНИКА

В специальной теории относительности рассматриваются только инерциальные системы отсчета. Во всех задачах считается, что оси у, у' и z, z' сонаправлены, а относительная скорость v₀ системы координат К' относительно системы К направлена вдоль общей оси хх'.

• Релятивистское (лоренцево) сокращение длины стержня:

где l₀ — длина стержня в системе координат К',относительно которой стержень покоится (собственная длина). Стержень параллелен оси х'; l — длина стержня, измеренная в системе К,относительно которой он движется со скоростью ; с — скорость распространения электромагнитного излучения.

• Релятивистское замедление хода часов

,

где Δt₀ — интервал времени между двумя событиями, происходящими в одной точке системы , измеренный по часам этой системы (собственное время движущихся часов); Δt — интервал времени между двумя событиями, измеренный по часам системы K.

• Релятивистское сложение скоростей

,

где — относительная скорость (скорость тела относительно системы K'); 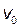— переносная скорость (скорость системы K' относительно К), — абсолютная скорость (скорость тела относительно системы К).

В теории относительности абсолютной скоростью называется скорость тела в системе координат, условно принятой за неподвижную.

• Релятивистский импульс:

.

• Полная энергия релятивистской частицы

,

где T — кинетическая энергия частицы; 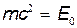— ее энергия покоя. Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если .

• Связь полной энергии с импульсом релятивистской частицы:

.

• Связь кинетической энергии с импульсом релятивистской частицы

.

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

• Уравнение гармонических колебаний:

где х — смещение колеблющейся точки от положения равновесия;
t — время; А, ω, φ— соответственно амплитуда, угловая частота,
начальная фаза колебаний; 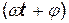— фаза колебаний в момент t.

• Угловая частота колебаний:

, или ,

где ν и Т — частота и период колебаний.

• Скорость точки, совершающей гармонические колебания:

.

• Ускорение при гармоническом колебании

.

• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле:

где А₁и А₂— амплитуды составляющих колебаний; φ₁ и φ₂— их начальные фазы.

• Начальная фаза φ результирующего колебания может быть найдена из формулы:

.

• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν₁ и ν₂,

.

• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами A₁ и A₂ и начальными фазами φ₁ и φ₂:

.

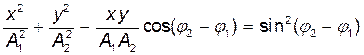• Дифференциальное уравнение гармонических колебаний материальной точки:

, или ,

где m — масса точки; k — коэффициент квазиупругой силы ( ).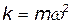

• Полная энергия материальной точки, совершающей гармонические колебания:

.

• Период колебаний тела, подвешенного на пружине (пружин­ный маятник):

,

где m — масса тела; k — жесткость пружины. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).

Период колебаний математического маятника

,

где l — длина маятника; g — ускорение свободного падения.

Период колебаний физического маятника

,

где J — момент инерции колеблющегося тела относительно оси колебаний; а — расстояние центра масс маятника от оси колебаний; — приведенная длина физического маятника.

Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более ошибка в значении периода не превышает 1 %.

Период крутильных колебаний тела, подвешенного на упругой нити:

,

где J — момент инерции тела относительно оси, совпадающей с упругой нитью; K — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.

• Дифференциальное уравнение затухающих колебаний
или ,

где r — коэффициент сопротивления; δ — коэффициент затухания: ; ω₀— собственная угловая частота колебаний .

• Уравнение затухающих колебаний:

где A(t) — амплитуда затухающих колебаний в момент t; ω — их угловая частота.

• Угловая частота затухающих колебаний:

.

• Зависимость амплитуды затухающих колебаний от времени

,

где А₀ — амплитуда колебаний в момент t=0.

• Логарифмический декремент колебаний:

,

где A(t) и A(t+T) — амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.

• Дифференциальное уравнение вынужденных колебаний

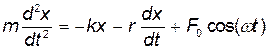или ,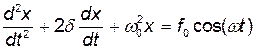

где — внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F₀ — ее амплитудное значение; .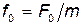

• Амплитуда вынужденных колебаний:

.

• Резонансная частота и резонансная амплитуда:

и .