Контрольная работа № 1.

Задачи

1. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом 60⁰ к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1,7 с.

2. Две частицы движутся с ускорением g в однородном поле силы тяжести. В начальный момент частицы находились в одной точке и имели скорости 3 м/с и 4 м/с, направленные горизонтально и в противоположные стороны. Найти расстояние между частицами в момент, когда векторы их скоростей окажутся взаимно перпендикулярными.

3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с². Через 2 с после начала подъема с потолка кабины стал падать болт. Найти: а) время свободного падения болта; б) перемещение и путь болта за время свободного падения в системе отсчета, связанной с шахтой лифта.

4. В момент времени t=0 частица вышла из начала координат в противоположном направлении оси x. Ее скорость меняется по закону 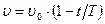, где 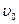- вектор начальной скорости, модуль которого см/с, Т=5 с. Найти: а) координату х частицы в моменты времени 6 с, 10 с и 20 с; б) момент времени, когда частица будет находиться на расстоянии 10 см от начала координат; в) путь S, пройденный частицей за первые 4 и 8 с; изобразить примерный график S(t).

5. Материальная точка движется прямолинейно с ускорением а=5 м/с². Определить на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять .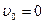

6. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью 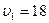км/ч. Далее половину оставшегося времени он ехал со скоростью 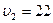км/ч, после чего до конечного пункта он шел пешком со скоростью км/ч. Определить среднюю скорость велосипедиста.

7. Тело брошено с начальной скоростью с высоты h=2,4 м вверх под углом 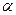=35⁰ к горизонту и упало на расстоянии l=37 м от места бросания. Найти начальную скорость тела.

8. Тело брошено с вышки в горизонтальном направлении со скоростью 20 м/с. Определить скорость тела и ее направление в конце второй секунды после начала движения.

9. Твердое тело вращается вокруг неподвижной оси по закону , где а=6 рад/с, b=2 рад/с³. Найти: а)средние значения угловой скорости и углового ускорения за промежуток времени от начала вращения до остановки; б) угловое ускорение в момент остановки тела.

10. Точка движется по окружности радиусом R= 30 см с постоянным угловым ускорением. Определить тангенциальное ускорение 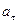точки, если известно, что за время 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение =2,7 м/с².

11. На верхнем конце наклонной плоскости укреплен легкий блок, через который перекинута нить с грузами m₁=5,1 кг и m₂=2,2 кг на концах. Груз m₁ скользит вниз по наклонной плоскости, поднимая висящий на другом конце нити груз m₂. Угол наклонной плоскости с горизонтом 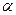=37⁰, коэффициент трения между грузом m₁ и плоскостью равен 0,1. Определить ускорение грузов.

12. На верхнем конце наклонной плоскости укреплен легкий блок, через который перекинута нить с грузами m₁=1,7 кг и m₂=0,4 кг на концах. Груз m₁ скользит вниз по наклонной плоскости, поднимая висящий на другом конце нити груз m₂. Угол наклонной плоскости с горизонтом 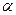=48⁰, ускорение грузов а=2,1 м/с². Определить коэффициент трения между грузом m₁ и плоскостью.

13. На разных склонах наклонной плоскости, образующих с горизонтом углы 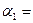32⁰ и 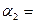48⁰, находятся грузы m₁=3,3 кг и m₂. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,1, ускорение грузов а= - 1,2 м/с² (а > 0, если система движется в сторону груза m₂). Определить массу второго груза m₂.

14. На разных склонах наклонной плоскости, образующих с горизонтом углы 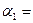65⁰и 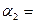35⁰, находятся грузы m₁=4,8 кг и m₂=5,6 кг. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,12, ускорение грузов а (а > 0, если система движется в сторону груза m₂). Определить массу второго груза m₂. Определить ускорение грузов а.

15. Шарик массой m=45 г падает на горизонтальную поверхность стола с высоты h₁=2,4 м и, отскочив, поднимается на некоторую высоту h₂. Время соударения t=0,49 мс, средняя сила взаимодействия шарика со столом F=1200 Н.

Шарик массой m падает на горизонтальную поверхность стола с высоты h₁=1,9 м и, отскочив, поднимается на высоту h₂=1,5 м. Время соударения t=0,18 мс, средняя сила взаимодействия шарика со столом F=270 Н.

16. Через блок перекинута нить, к концам которой подвешены гири массами m₁=m₂=1 кг. Какую силу нужно приложить к одной из гирь, чтобы гири стали двигаться с ускорением а=3 м/с². Массой блока пренебречь.

17. Автомобиль массой m=5000 кг движется со скоростью 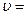10 м/с по выпуклому мосту. Определить силу давления автомобиля на мост в его верхней точке, если радиус кривизны моста R=50 м.

18. Какую наибольшую скорость может развивать велосипедист, проезжая закругление R=50 м, если коэффициент трения скольжения между шинами и асфальтом равен 0,3? Каков угол отклонения 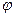велосипеда от вертикали, когда велосипедист движется по закруглению?

19. Тело, двигаясь равноускоренно, соскользнуло с наклонной плоскости длиной l=2 м за время t=2 c. Определить коэффициент трения тела о плоскость. Угол наклона 30⁰.

20. Две лодки массами m₁=250 кг и m₂=370 кг идут параллельными курсами со скоростями 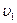=1,6 м/с и 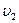. Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m=32 кг, после чего лодки продолжают двигаться параллельными курсами, но со скоростями u₁ и u₂=2,1 м/с. Найти скорость u₁.

21. Две лодки массами m₁=310 кг и m₂=160 кг идут параллельными курсами со скоростям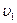и и 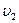. Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m=25 кг, после чего лодки продолжают двигаться параллельными курсами, но со скоростями u₁= -1,7 м/с и u₂=2,8 м/с. Найти скорость .

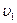22. Снаряд, летящий со скоростью 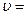750 м/с, разрывается на два осколка массами m₁=45 кг и m₂=17 кг, разлетающиеся под углом 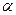со скоростями u₁= 710 м/с и u₂=900 м/с. Определить угол .

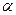23. Снаряд, летящий со скоростью 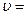550 м/с, разрывается на два осколка массами m₁=14 кг и m₂=8 кг, разлетающиеся под углом 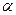=95⁰ со скоростями u₁ и u₂=830 м/с. Определить скорость u₁.

24. Человек массы m₁=55 кг, стоящий на одном конце первоначально покоящейся тележки масс m₂=120 кг и длины l=4,5 м, прыгает со скоростью относительно земли под углом 25⁰ к горизонту и попадает на другой конец тележки. Массу колес, а также силы сопротивления движению тележки не учитывать. Определить скорость .

25. Человек массы m₁=45 кг, стоящий на одном конце первоначально покоящейся тележки масс m₂=160 кг и длины l=3,5 м, прыгает со скоростью 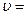5,5 м/с относительно земли под углом 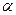к горизонту и попадает на другой конец тележки. Массу колес, а также силы сопротивления движению тележки не учитывать. Определить угол .

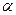26. В деревянный шар массой m₁=8 кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля m₂=4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в ней пулей отклонилась от вертикали на угол 3⁰? Размером шара пренебречь. Удар пули считать прямым, центральным.

27. Шар массой m₁=5 кг движется со скоростью 1 м/с и сталкивается с покоящимся шаром массой m₂=2 кг. Определить скорости шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

28. Шар массой m₁=2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу m₂ большего шара. Удар считать абсолютно упругим, прямым, центральным.

29. Два груза массами m₁=10 кг и m₂=15 кг подвешены на нитях длиной l=2 м так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол 60⁰ и отпущен. На какую высоту поднимутся оба груза после удара? Удар считать неупругим.

30. Шайба массы m=50 г соскальзывает без начальной скорости по наклонной плоскости, составляющий угол 30⁰ с горизонтом, и, пройдя по горизонтальной плоскости расстояние l=50 см, останавливается. Найти работу сил трения на всем пути, считая всюду коэффициент трения 0,15.

31. Из пружинного пистолета с жесткостью пружины k=150 Н/м был произведен выстрел пулей массой m=8 г. Определить скорость пули при выстреле ее из пистолета, если пружина была сжата на 4 см.

32. Молот массой m₁=5 кг ударяет о небольшой кусок железа, лежащий на наковальне. Масса наковальни m₂=100 кг. Массой куска железа пренебречь. Удар неупругий. Определить КПД удара молота при данных условиях.

33. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то она сожмется на 3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты 8 см?

34. Определить работу растяжения двух последовательно соединенных пружин жесткостями k₁=0,5 кН/м и k₂=1 кН/м, если первая пружина при этом растянулась на 2 см.

35. Две пружины жесткостями k₁=400 Н/м и k₂=250 Н/м соединены параллельно. Определить потенциальную энергию данной системы при абсолютной деформации 4 см.

36. Из шахты глубиной h=600 м поднимают клеть массой m=3 т на канате, каждый метр которого имеет массу m₁=1,5 кг. Какая работа совершается при поднятии клети на поверхность Земли? Каков КПД подъемного устройства.

37. Налетев на пружинный буфер, вагон массой m=16 т, двигавшийся со скоростью 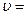0,6 м/с, остановился, сжав пружину на 8 см. Найти общую жесткость пружин буфера.

38. Цепь длиной l=2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает 1/3 длины цепи, то цепь соскальзывает со стола. Определить скорость цепи в момент ее отрыва от стола.

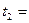39. Материальная точка массой m=2 кг двигалась под действием некоторой силы согласно уравнению , где А=10 м, В= - 2 м/с, С=1 м/с², D= - 0,2 м/с³. Найти мощность, развиваемую при движении, в моменты времени 2 c и 5 c.

40. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную точку? Масса платформы m₁=240 кг, масса человека m₂=60 кг. Момент инерции человека рассчитывать как для материальной точки.

41. Маховик, вращающийся с постоянной угловой скоростью 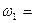62,8 рад/с, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова сделалось равномерным, но уже с угловой скоростью 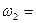37,7 рад/с. Определить угловое ускорение маховика и продолжительность торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов.

42. Платформа в виде сплошного диска радиусом R=1,5 м и массой m₁=180 кг вращается по инерции около вертикальной оси с частотой 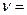10 об/мин. В центре платформы стоит человек массой m₂=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

43. По касательной к шкиву маховика в виде диска диаметром D=75 см и массой m=40 кг приложена сила F=10 Н. Определить угловое ускорение и частоту вращения маховика через 10 с после начала действия силы, если радиус шкива R= 12 см. Силой трения пренебречь.

44. Нить с привязанными к ее концам грузами массой m₁=50 г и m₂=60 г перекинута через блок диаметром D=4 см. Определить момент инерции блока, если под действием силы тяжести грузов он получил угловое ускорение 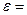1,5 рад/с².

45. Маховик в виде диска массой m=50 кг и радиусом R=20 см был раскручен до угловой скорости 50 рад/с и затем предоставлен самому себе. Под влиянием трения маховик остановился. Найти момент сил трения, считая его постоянным, принимая во внимание, что: а) маховик остановился через 50 с; б) маховик остановился и до полной остановки сделал 200 оборотов.

46. На краю платформы в виде диска диаметром D=2 м, вращающийся по инерции вокруг вертикальной оси с частотой 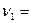0,13 Гц, стоит человек массой m=70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой 0,16 Гц. Определить массу платформы.

47. Платформа в виде диска диаметром D=3 м и массой m₁=180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться платформа, если по ее краю пойдет человек массы m₂=70 кг со скоростью 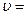1,8 м/с относительно платформы.

48. Блок, имеющий форму диска массой m=0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m₁=0,3 кг и m₂=0,7 кг. Определить силы натяжения нити по обе стороны блока.

49. На краю неподвижной скамьи Жуковского диаметром D=0,2 м и массой m₁=6 кг стоит человек массой m₂=60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой m₃=0,5 кг?

50. Маховик в виде сплошного диска радиусом R=20 см и массой m=50 кг раскручен до частоты вращения 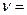8 Гц и предоставлен самому себе. Под действием силы трения маховик остановился через 50 с. Найти момент сил трения.

51. Маховик, массу которого m=5 кг можно считать распределенной по ободу радиуса R=20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой 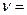12 Гц. При торможении маховик останавливается через 20 с. Найти тормозящий момент и число оборотов, которые сделает маховик до полной остановки.

52. Вал в виде сплошного цилиндра массой m₁=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m₂=2 кг. С каким ускорением будет опускаться гиря, если ее предоставить самой себе?

53. Сплошной цилиндр массой m=4 кг катится без скольжения по горизонтальной поверхности. Линейная скорость оси цилиндра 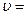1 м/с. Определить полную кинетическую энергию цилиндра.

54. Обруч и сплошной цилиндр, имеющие одинаковую массу m=2 кг, катятся без скольжения с одинаковой скоростью 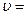5 м/с. Найти кинетические энергии этих тел.

55. Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия шара 14 Дж. Определить кинетическую энергию поступательного и вращательного движения шара.

56. Определить линейную скорость центра шара, скатившегося без скольжения с наклонной плоскости высотой h=1 м.

57. Сколько времени будет скатываться без скольжения обруч с наклонной плоскости длиной l=2 м и высотой h=0,1 м.

58. Якорь мотора вращается с частотой 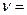1500 об/мин. Определить вращающий момент, если мотор развивает мощность N=500 Вт.

59. Пуля массой m=10 г летит со скоростью 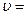800 м/с, вращаясь около продольной оси с частотой 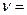3000 об/с.Принимая пулю за цилиндрик диаметра D=8 мм, определить полную кинетическую энергию пули.

60. Уравнение колебаний точки имеет вид: 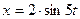. Определить максимальные значения скорости и ускорения точки.

61. Точка совершает гармонические колебания по закону . В какой момент времени ее потенциальная энергия равна кинетической энергии?

62. Тело массой m совершает колебания по закону 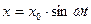. Определить силу, действующую на тело, и его максимальную кинетическую энергию.

63. Материальная точка массой m=50 г совершает гармонические колебания согласно уравнению 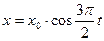м.Определить: а) возвращающую силу F для момента времени t=0,5 с; б) полную энергию точки.

64. Математический маятник массой m=10 г и длиной l=10 м совершает гармонические колебания по закону 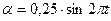. Определить силу натяжения в момент времени t=T/2.

65. Физический маятник совершает гармонические колебания около горизонтальной оси с периодом Т₁=1,75 с. Если к нему прикрепить небольшой груз массы m=0,85 кг на расстоянии l ниже оси, то период колебаний будет равен Т₂=2,05 с. Момент инерции маятника относительно оси J=620 кг∙см².

66. За время t=75 c полная механическая энергия математического маятника длины l=0,85 м уменьшилась в k раз. Период собственных колебаний маятника равен Т, логарифмический декремент затухания 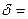0,011.Определить k.

67. Начальная амплитуда колебаний математического маятника А₁=0,2 м. Амплитуда после 10 полных колебаний А₁₀=0,01 м. Определить логарифмический декремент затухания и коэффициент затухания, если период колебаний Т=5 с. Записать уравнение колебаний.

68. Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями см и 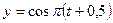см. Найти уравнение траектории и построить ее на чертеже, показав направление движения точки.

69. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнения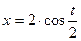ми см и 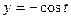см. Найти уравнение траектории и построить ее на чертеже.

70. Ракета движется относительно земного наблюдателя со скоростью 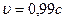. Какое время пройдет по часам земного наблюдателя, если по часам в ракете прошло 10 лет?

71. Два космических корабля стартуют с Земли в противоположных направлениях, каждый со скоростью 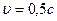относительно Земли. Найти: а) чему равна скорость первого космического корабля относительно второго? б) чему равна скорость второго космического корабля относительно первого?

72. Две релятивистские частицы движутся в лабораторной системе отсчета со скоростями и 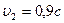вдоль одной прямой. Определить их относительную скорость 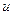в двух случаях: а) частицы движутся в одном направлении; б) частицы движутся в противоположных направлениях.

73. Найти скорость частицы, если ее кинетическая энергия составляет половину энергии покоя.

74. При какой скорости энергия тела на 1% превышает его энергию покоя?

75. Электрон движется со скоростью . Определить релятивистский импульс электрона.

76. Вычислить кинетическую энергию и импульс протона, летящего со скоростью 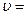8,3∙10⁷ м/с. На сколько процентов вы ошибетесь, если воспользуетесь классическими формулами? Масса протона 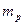=1,67∙10²⁷ кг.

77. Определить скорость электрона, если его кинетическая энергия: а) Т=4 МэВ; б) Т=1 кэВ. В каком из этих случаев можно было бы применить классическую формулу ?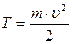

78. Определить кинетическую энергию релятивистской частицы (в единицах ), если ее импульс .

79. Импульс релятивистской частицы .Определить скорость частицы (в долях скорости света).

80. Электрон движется со скоростью 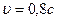. Определить релятивистский импульс электрона.

ГИДРОДИНАМИКА

· Расход жидкости в трубке тока:

а) объемный расход ;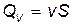

б) массовый расход 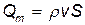, где S – площадь поперечного сечения трубки тока; v – скорость жидкости; 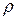– ее плотность.

· Уравнение неразрывности струи:

,

где S₁ и S₂ – площади поперечного сечения трубки тока в двух местах; v₁ и v₂ – соответствующие скорости течений.

· Уравнение Бернулли для идеальной несжимаемой жидкости в общем случае

,

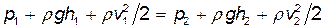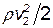где p₁ и p₂ – статические давления жидкости в двух сечениях трубки тока; v₁ и v_{2 –}скорости жидкости в этих сечениях; и – динамические давления жидкости в этих же сечениях; h₁и h₂ – высоты их над некоторым уровнем; и 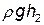– гидростатические давления.

· Скорость течения жидкости из малого отверстия в открытом широком сосуде:

,

где h — глубина, на которой находится отверстие относительно уровня жидкости в сосуде.

· Формула Пуазейля. Объем жидкости (газа), протекающей за время t через длинную трубку:

,

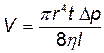где r — радиус трубки; l – ее длина; Δp – разность давлений на концах трубки; η – динамическая вязкость (коэффициент внутреннего трения) жидкости.

· Число Рейнольдса для потока жидкости в длинных трубках:

,

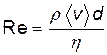где <v> – средняя по сечению скорость течения жидкости; d – диаметр трубки, и для движения шарика в жидкости:

,

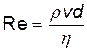где v – скорость шарика; d—его диаметр.

Число Рейнольдса Re есть функция скорости v тела, линейной величины l, определяющей размеры тела, плотности 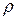и динамической вязкости η жидкости, т. е. .

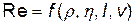При малых значениях чисел Рейнольдса, меньших некоторого критического значения , движение жидкости является ламинарным. При значениях движение жидкости переходит в турбулентное.

Критическое число Рейнольдса для движения шарика в жидкости ; для потока жидкости в длинных трубках .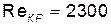

· Формула Стокса. Сила сопротивления F, действующаясо стороны потока жидкости на медленно движущийся в ней шарик:

,

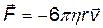где r – радиус шарика; v – его скорость.

Формула справедлива для скоростей, при которых число Рейнольдса много меньше единицы ( ).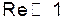

УПРУГИЕ ДЕФОРМАЦИИ ТВЕРДОГО ТЕЛА

• Относительная деформация при продольном растяжении или сжатии тела:

,

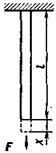
где 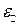— относительное удлинение (сжатие); x — абсолютное удлинение (рис. 4.1); l — начальная длина тела.

Относительная деформация при сдвиге определяется из формулы:

,

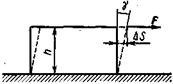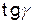где — относительный сдвиг; Δs — абсолютный сдвиг параллельных слоев тела относительно друг друга; h — расстояние между- слоями; 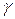— угол сдвига. (Для малых углов )

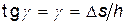• Напряжение нормальное:

,

где 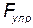— упругая сила, перпендикулярная поперечному сечению тела; S — площадь этого сечения.

Напряжение тангенциальное:

,

где 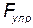— упругая сила, действующая вдоль слоя тела; S — площадь этого слоя.

• Закон Гука для продольного растяжения или сжатия:

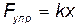или ,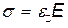

где k — коэффициент упругости (в случае пружины — жесткость); Е — модуль Юнга.

Закон Гука для сдвига:

,

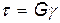где G — модуль поперечной упругости (модуль сдвига).

• Момент, закручивающий на угол φ однородный круглый стержень:

,

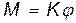где — постоянная кручения.

• Потенциальная энергия растянутого или сжатого стержня при однородной деформации:

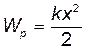или ;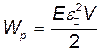

при неоднородной деформации: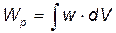

где V — объем тела; объемная плотность энергии растянутого или сжатого стержня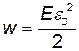

ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ

· Количество вещества — число структурных элементов (молекул, атомов, ионов и т. п ), содержащихся в системе или теле. Количество вещества выражается в молях. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в изотопе углерода 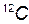массой 0,012 кг. Количество вещества:

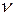=N/N_A

где N — число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); N_A — постоянная Авогадро:

N_A =6,02×10²³ моль^-1.

· Молярная масса вещества:

,

где m — масса однородного тела (системы); 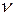— количество вещества этого тела.

· Относительная молекулярная масса вещества:

,

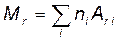где n_i — число атомов i-го химического элемента, входящего в состав молекулы данного вещества; 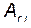— относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева.

· Связь молярной массы М с относительной молекулярной массой M_r вещества:

,

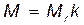где k=10^-3 кг/моль.

· Молярная масса смеси газов

,

где m_i — масса i-го компонента смеси; v_i — количество вещества i-го компонента смеси; k — число компонентов смеси.

· Массовая доля i-го компонента смеси газов

,

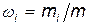где m_i — масса i-го компонента смеси; m — масса смеси.

· Уравнение состояния идеальных газов (уравнение Клапейрона — Менделеева)

или ,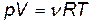

где m — масса газа; М — его молярная масса; R — молярная газовая постоянная; Т — термодинамическая температура; 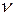— количество вещества.

· Закон Дальтона:

,

где p — давление смеси газов; p_i — парциальное давление i-го компонента смеси; k — число компонентов смеси.

· Концентрация частиц (молекул, атомов и т. п.) однородной системы

,

где V — объем системы.

ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ

· Связь между молярной ( 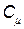) и удельной (с) теплоемкостями газа

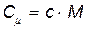,где М — молярная масса газа.

· Молярные теплоемкости при постоянном объеме и постоянном давлении соответственно равны (в целях упрощения записи в индексах обозначений молярной теплоемкости при постоянном давлении и постоянном объеме букву « 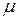» будем опускать)

; ,

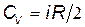где 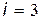для газа одноатомных молекул, 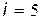для газа двухатомных молекул, 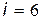для газа трех- и более атомных молекул; 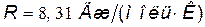— молярная газовая постоянная.

· Уравнение Майера

.

· Показатель адиабаты

.

· Внутренняя энергия идеального газа

,

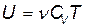где — количество вещества.

· Работа, связанная с изменением объема газа, в общем случае вычисляется по формуле

,

где V₁ — начальный объем газа; V₂ — его конечный объем.

Работа газа:

а) при изобарном процессе (p=const)

;

б) при изотермическом процессе (T=const)

;

в) при адиабатном процессе

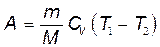, или ,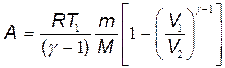

где T₁ — начальная температура газа; T₂ — его конечная температура.

· Уравнение Пуассона (уравнение газового состояния при адиабатном процессе)

.

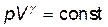· Связь между начальным и конечным значениями параметров состояний газа при адиабатном процессе:

.

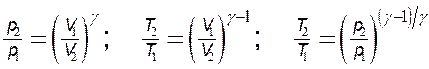· Первое начало термодинамики в общем случае записывается в виде

Q=DU+A,

где Q – количество теплоты, сообщённое газу; DU—изменение его внутренней энергии; А — работа, совершаемая газом против внешних сил.

Первое начало термодинамики:

а) при изобарном процессе

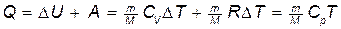
б) при изохорном процессе (A=0)

;

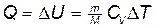в) при изотермическом процессе (DU=0)

,

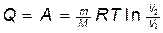г) при адиабатном процессе (Q=0)

.

· Термический коэффициент полезного действия (КПД) цикла в общем случае

,

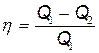где Q₁ – количество теплоты, полученное рабочим телом (газом) от нагревателя; Q₂ – количество теплоты, переданное рабочим телом охладителю.

КПД цикла Карно

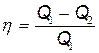, или ,

где T₁ — температура нагревателя; T₂ — температура охладителя.

· Изменение энтропии

где A и B — пределы интегрирования, соответствующие начальному и конечному состояниям системы. Так как процесс равновесный, то интегрирование проводится по любому пути.