
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач 2 страница
3. Сравнение кинетических энергий шаров до и после удара показывает, что в результате неупругого удара шаров произошло уменьшение их кинетической энергии, за счет чего увеличилась их внутренняя энергия. Долю кинетической энергии шаров, пошедшей на увеличение их внутренней энергии, определим из соотношения:

Пример 10. Шар массой m1, движущийся горизонтально с некоторой скоростью v1, столкнулся с неподвижным шаром массой т2. Шары абсолютно упругие, удар прямой. Какую долю  своей кинетической энергии первый шар передал второму?
своей кинетической энергии первый шар передал второму?
Решение. Доля энергии, переданной первым шаром второму, выразится соотношением:
 (1)
(1)
где  — кинетическая энергия первого шара до удара; u2 и
— кинетическая энергия первого шара до удара; u2 и 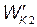 ,— скорость и кинетическая энергия второго шара после удара.
,— скорость и кинетическая энергия второго шара после удара.
Как видно из выражения (1), для определения  надо найти u2. Воспользуемся тем, что при ударе абсолютно упругих тел одновременно выполняются два закона сохранения: импульса и механической энергии.
надо найти u2. Воспользуемся тем, что при ударе абсолютно упругих тел одновременно выполняются два закона сохранения: импульса и механической энергии.
По закону сохранения импульса, учитывая, что второй шар до удара покоился, имеем 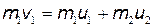 . По закону сохранения энергии в механике,
. По закону сохранения энергии в механике,  Решая совместно два последних уравнения, найдем:
Решая совместно два последних уравнения, найдем:
u2=2m1v1/(m1+m2).
Подставив это выражение u2 в равенство (1), получим:

Из этого соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменяются местами.
Пример 11. Боек (ударная часть) свайного молота массой т1=500 кг падает на сваю массой m2=100 кг со скоростью v1=4 м/с. Определить: 1) кинетическую энергию  бойка в момент удара; 2) энергию
бойка в момент удара; 2) энергию  , затраченную на углубление сваи в грунт; 3) кинетическую энергию
, затраченную на углубление сваи в грунт; 3) кинетическую энергию  , перешедшую во внутреннюю энергию системы; 4) КПД
, перешедшую во внутреннюю энергию системы; 4) КПД  удара бойка о сваю. Удар бойка о сваю рассматривать как неупругий.
удара бойка о сваю. Удар бойка о сваю рассматривать как неупругий.
Решение. 1. Кинетическую энергию бойка в момент удара о сваю находим по формуле  =m1v12/2. Подставив значения m1, и v1 и произведя вычисления, получим:
=m1v12/2. Подставив значения m1, и v1 и произведя вычисления, получим:
 =(500×42)/2 Дж=4000 Дж=4 кДж.
=(500×42)/2 Дж=4000 Дж=4 кДж.
2. Чтобы определить энергию, затраченную на углубление сваи, предварительно найдем скорость системы боек — свая непосредственно после удара. Для этого применим закон сохранения импульса, который в случае неупругого удара выражается формулой:
т1v1+m2v2=(m1+m2)u, (1)
где v2 — скорость сваи перед ударом; и — скорость бойка и сваи непосредственно после удара. Свая перед ударом находилась в состоянии покоя, поэтому v2=0. Так как удар неупругий, то боек и свая после удара движутся как одно целое, т. е. с одинаковой скоростью и. Из формулы (1) найдем эту скорость:
 (2)
(2)
В результате сопротивления грунта скорость бойка и сваи после удара быстро гасится, а кинетическая энергия, которой обладает система боек — свая, затрачивается на углубление сваи в грунт.
Эту энергию находим по формуле  Заменим скорость и ее выражением (2):
Заменим скорость и ее выражением (2):  или, учитывая, что
или, учитывая, что  =m1v12/2, запишем:
=m1v12/2, запишем:
 (3)
(3)
Подставив в формулу (3) значения т1, m2 и  и произведя вычисления, получим:
и произведя вычисления, получим:
 = [500/(500+100)]. 4·103 Дж=3,33·103 Дж=3,33 кДж.
= [500/(500+100)]. 4·103 Дж=3,33·103 Дж=3,33 кДж.
3. Боек до удара обладал энергией  ;
;  — энергия, затраченная на углубление сваи в грунт. Следовательно, во внутреннюю энергию, связанную с неупругой деформацией сваи, превратилась энергия:
— энергия, затраченная на углубление сваи в грунт. Следовательно, во внутреннюю энергию, связанную с неупругой деформацией сваи, превратилась энергия:
 =
=  —
—  .
.
Подставив в это выражение значения T1 и T2, найдем
 =0,67 кДж.
=0,67 кДж.
4. Свайный молот служит для забивки сваи в грунт; следовательно, энергию  следует считать полезной. КПД удара бойка о сваю выразится как отношение энергии
следует считать полезной. КПД удара бойка о сваю выразится как отношение энергии  , затраченной на углубление сваи в грунт, ко всей затраченной энергии
, затраченной на углубление сваи в грунт, ко всей затраченной энергии  :
:
 =
=  /
/  .
.
Подставив в последнее выражение  по формуле (3), получим
по формуле (3), получим
 =m1/(m1+m2).
=m1/(m1+m2).
Подставим значения m1 и т2и произведем вычисления:
 =83,3%.
=83,3%.
Пример 12. Вычислить момент инерции Jz молекулы NО2 относительно оси z, проходящей через центр масс молекулы перпендикулярно плоскости, содержащей ядра атомов. Межъядерное расстояние d этой молекулы равно 0,118 нм, валентный угол  =140°.
=140°.
Решение. Молекулу NO2 можно рассматривать как систему, состоящую из трех материальных точек общей массой
m=2m1+m2, (1)
где m1 — масса атома кислорода; m2 — масса атома азота.
Расположим молекулу относительно координатных осей так, как это указано на рис. 8 (начало координат совместим с центром масс С молекулы, ось z направим перпендикулярно плоскости чертежа «к нам».)
Для определения Jz воспользуемся теоремой Штейнера:
J=Jc+ma2.
 Для данного случая эта теорема запишется в виде Jz' = Jz+ma2, где Jz' —момент инерции относительно оси z', параллельной оси z и проходящей через атом азота (точка О на рис. 8). Отсюда искомый момент инерции
Для данного случая эта теорема запишется в виде Jz' = Jz+ma2, где Jz' —момент инерции относительно оси z', параллельной оси z и проходящей через атом азота (точка О на рис. 8). Отсюда искомый момент инерции
Jz = Jz' –ma2 (2)
 Момент инерции Jz' находим как сумму моментов инерции двух материальных точек (атомов кислорода):
Момент инерции Jz' находим как сумму моментов инерции двух материальных точек (атомов кислорода):
Jz' = 2m1 d2 (3)
Расстояние а между осями z и z' равно координате xс центра масс системы и поэтому может быть выражено по формуле:
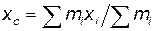 .
.
В данном случае:
а=хс= (2m1x1+m2x2)/(2m1+m2),
или, учитывая, что x1=d cos (  /2) и х2=0,
/2) и х2=0,
 (4)
(4)
Подставив в формулу (2) значения Jz', т, а соответственно из выражений (3), (1), (4), получим:

или после преобразований:
 (5)
(5)
Относительные атомные массы кислорода (AO=16) и азота (АN=14). Запишем массы атомов этих элементов в атомных единицах массы (а.е.м.), а затем выразим в килограммах (1 а.е.м. =1,66 ·10-27 кг):
m1= 161,66·10-27 кг=2,66·10-26 кг;
m2 = 141,66·10-27 кг = 2,32·10-26 кг.
Значения m1, т2, d и  подставим в формулу (5) и произведем вычисления:
подставим в формулу (5) и произведем вычисления:
Jz=6,80·10-46 кг·м2.
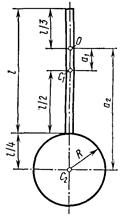
Пример 13. Физический маятник представляет собой стержень длиной l =1 м и массой m1=l кг с прикрепленным к одному из его концов диском массой т2=0,5 m1. Определить момент инерции Jzтакого маятника относительно оси Оz, проходящей через точку О на стержне перпендикулярно плоскости чертежа (рис. 9).
|
Решение. Общий момент инерции маятника равен сумме моментов инерции стержня Jz1 и диска Jz2.
Jz = Jz1 + Jz2 (1)
Формулы, по которым вычисляются моменты инерции стержня Jz1 и диска Jz2 относительно осей, проходящих через их центры масс, даны в табл. на с. 13. Чтобы определить моменты инерции Jz1 и Jz2, надо воспользоваться теоремой Штейнера:
J=Jc+ma2. (2)
 Выразим момент инерции стержня согласно формуле (2):
Выразим момент инерции стержня согласно формуле (2):
Jz1=l/12m1l2+m1a12.
Расстояние a1 между осью Оz и параллельной ей осью, проходящей через центр масс C1 стержня, как следует из рис. 9, равно 1/2l ‑ l/3l=l/6l. С учетом этого запишем:
Jz1=l/12m1l2+m1 (l/6l )2=1/9m1l2=0,111m1l2.
Момент инерции диска в соответствии с формулой (2) равен:
Jz2=l/2m2R2+m2a22.
где R — радиус диска; R=1/4l. Расстояние а2 между осью Оz и параллельной ей осью, проходящей через центр масс диска, равно (рис. 9) 2/3l + l/4l=l1/12l. С учетом этого запишем:
Jz2=l/2m2 (1/4l)2+m2(l1/12l)2= 0,0312 m2l2 + 0,840 m2l2= 0,871 m2l2.
Подставив полученные выражения Jz1 и Jz2 в формулу (1), найдем
Jz=0,111m1l2+0,871 m2l2=(0,111m1+0,871 m2)l2,
или, учитывая, что т2=0,5 m1,
Jz=0,547m1l2.
Произведя вычисления, получим значение момента инерции физического маятника относительно оси Оz:
Jz =0,547·1·1 кг·м2=0,547 кг·м2.
Пример 14. Вал в виде сплошного цилиндра массой m1=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m2=2 кг (рис. 10). С каким ускорением а будет опускаться гиря, если ее предоставить самой себе?
Решение. Линейное ускорение а гири равно тангенциальному ускорению точек вала, лежащих на его цилиндрической поверхности,
и связано с угловым ускорением  вала соотношением:
вала соотношением:
 , (1)
, (1)
где r — радиус вала.
Угловое ускорение вала выражается основным уравнением динамики вращающегося тела:
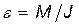 , (2)
, (2)

|
где М — вращающий момент, действующий на вал; J — момент инерции вала. Рассматриваем вал как однородный цилиндр. Тогда его момент инерции относительно геометрической оси равен
J=1/2m1r2.
Вращающий момент М, действующий на вал, равен произведению силы натяжения Т шнура на радиус вала: М=Тr.
 Силу натяжения шнура найдем из следующих соображений. На гирю действуют две силы: сила тяжести
Силу натяжения шнура найдем из следующих соображений. На гирю действуют две силы: сила тяжести  , направленная вниз, и сила натяжения
, направленная вниз, и сила натяжения  шнура, направленная вверх. Равнодействующая этих сил вызывает равноускоренное движение гири. По второму закону Ньютона, m2g – T=m2a, откуда T=m2(g – а). Таким образом, вращающий момент M=m2(g—а)r.
шнура, направленная вверх. Равнодействующая этих сил вызывает равноускоренное движение гири. По второму закону Ньютона, m2g – T=m2a, откуда T=m2(g – а). Таким образом, вращающий момент M=m2(g—а)r.
Подставив в формулу (2) полученные выражения М и J, найдем угловое ускорение вала:

Для определения линейного ускорения гири подставим это выражение  в формулу (1). Получим
в формулу (1). Получим
 ,
,
откуда
 .
.
Пример 15. Через блок в виде диска, имеющий массу m=80 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1=100 г и m2=200 г (рис. 11). С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
Решение. Применим к решению задачи основные законы поступательного и вращательного движения. На каждый из движущихся грузов действуют две силы: сила тяжести  , направленная вниз, и сила
, направленная вниз, и сила  натяжения нити, направленная вверх.
натяжения нити, направленная вверх.
 Так как вектор ускорения
Так как вектор ускорения  груза m1 направлен вверх, то T1>m1g. Равнодействующая этих сил вызывает равноускоренное движение и, по второму закону Ньютона, равна T1 – т1g=т1а, откуда:
груза m1 направлен вверх, то T1>m1g. Равнодействующая этих сил вызывает равноускоренное движение и, по второму закону Ньютона, равна T1 – т1g=т1а, откуда:
T1=m1g+m1a. (1)
Вектор ускорения  груза т2 направлен вниз; следовательно, T2<m2g. Запишем формулу второго закона для этого груза:
груза т2 направлен вниз; следовательно, T2<m2g. Запишем формулу второго закона для этого груза:
m2g – T2=m2a, откуда
T2=m2g – m2а. (2)
 Согласно основному закону динамики вращательного движения, вращающий момент М, приложенный к диску,равен произведению момента инерции J диска на его угловое ускорение
Согласно основному закону динамики вращательного движения, вращающий момент М, приложенный к диску,равен произведению момента инерции J диска на его угловое ускорение  :
:
M=J  . (3)
. (3)
Определим вращающий момент. Силы натяжения нитей действуют не только на грузы, но и на диск. По третьему закону Ньютона, силы 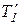 и
и 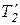 , приложенные к ободу диска, равны соответственно силам T1 и Т2, но по направлению им противоположны. При движении грузов диск ускоренно вращается по часовой стрелке; следовательно,
, приложенные к ободу диска, равны соответственно силам T1 и Т2, но по направлению им противоположны. При движении грузов диск ускоренно вращается по часовой стрелке; следовательно, 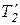 >
> 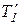 . Вращающий момент, приложенный к диску, равен произведению разности этих сил на плечо, равное радиусу диска, т. е. M=(
. Вращающий момент, приложенный к диску, равен произведению разности этих сил на плечо, равное радиусу диска, т. е. M=( 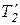 –
– 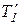 )r. Момент инерции диска J=mr2/2, угловое ускорение связано с линейным ускорением грузов соотношением
)r. Момент инерции диска J=mr2/2, угловое ускорение связано с линейным ускорением грузов соотношением 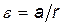 . Подставив в формулу (3) выражения М, J и
. Подставив в формулу (3) выражения М, J и  , получим
, получим
( 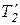 –
– 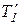 )r =
)r = 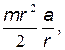
откуда
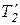 –
– 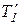 =(т/2)а.
=(т/2)а.
Так как 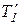 =T1 и
=T1 и 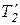 =Т2, то можно заменить силы
=Т2, то можно заменить силы 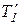 и
и 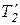 выражениями по формулам (1) и (2), тогда:
выражениями по формулам (1) и (2), тогда:
m2g – m2a – m1g – m1a=(m/2)a, или(m2—m1) g=(m2+m1+m/2)a
откуда:
 (4)
(4)
Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому значения масс m1, m2 и m можно выразить в граммах, как они даны в условии задачи. После подстановки получим:

Пример 16. Маховик в виде диска массой m=50 кг и радиусом r =20 см был раскручен до частоты вращения 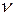 1=480 мин-1 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t=50 с; 2) маховик до полной остановки сделал N=200 оборотов.
1=480 мин-1 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t=50 с; 2) маховик до полной остановки сделал N=200 оборотов.
Решение. 1.По второму закону динамики вращательного движения, изменение момента импульса вращающегося тела равно произведению момента силы, действующего на тело, на время действия этого момента:
M 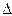 t=J
t=J  — J
— J  ,
,
где J — момент инерции маховика;  и
и  — начальная и конечная угловые скорости. Так как
— начальная и конечная угловые скорости. Так как  =0 и
=0 и  t=t , то Mt= – J
t=t , то Mt= – J  , откуда:
, откуда:
M= – J  /t. (1)
/t. (1)
Момент инерции диска относительно его геометрической оси равен J=1/2mr2. Подставив это выражение в формулу (1), найдем
M= – mr2  /(2t). (2)
/(2t). (2)
Выразив угловую скорость  через частоту вращения
через частоту вращения 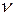 1 и произведя вычисления по формуле (2), найдем:
1 и произведя вычисления по формуле (2), найдем:
М= – 1 Н·м.
2. В условии задачи дано число оборотов, сделанных маховиком до остановки, т. е. его угловое перемещение. Поэтому применим формулу, выражающую связь работы с изменением кинетической энергии:

или, учтя, что  ,
,
 (3)
(3)
Работа при вращательном движении определяется по формуле A=Mj. Подставив выражения работы и момента инерции диска в формулу (3), получим:
M  = – mr2
= – mr2  /4.
/4.
Отсюда момент силы трения:
М= – mr2  /4
/4  . (4)
. (4)
Угол поворота j=2  N=2·3,14·200 рад=1256 рад. Произведя вычисления по формуле (4), получим:
N=2·3,14·200 рад=1256 рад. Произведя вычисления по формуле (4), получим:
М= – 1 Н·м.
Знак минус показывает, что момент силы трения оказывает тормозящее действие.
Пример 17. Платформа в виде диска радиусом R= 1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой 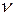 =10 мин-1. В центре платформы стоит человек массой т2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
=10 мин-1. В центре платформы стоит человек массой т2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
Решение. По закону сохранения момента импульса,
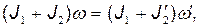 (1)
(1)
где J1 — момент инерции платформы; J2 — момент инерции человека, стоящего в центре платформы;  — угловая скорость платформы с человеком, стоящим в ее центре; J2' — момент инерции человека, стоящего на краю платформы;
— угловая скорость платформы с человеком, стоящим в ее центре; J2' — момент инерции человека, стоящего на краю платформы;  — угловая скорость платформы с человеком, стоящим на ее краю.
— угловая скорость платформы с человеком, стоящим на ее краю.
Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением:
 . (2)
. (2)
Определив  из уравнения (1) и подставив полученное выражение в формулу (2), будем иметь:
из уравнения (1) и подставив полученное выражение в формулу (2), будем иметь:
v=(J1+J2)  R/(J1+J'2). (3)
R/(J1+J'2). (3)
Момент инерции платформы рассчитываем как для диска; следовательно, J1=112m1R2. Момент инерции человека рассчитываем как для материальной точки. Поэтому J2=0, J'2=m2R2. Угловая скорость платформы до перехода человека равна  .
.
Заменив в формуле (3) величины J1, J2, J'2. и  их выражениями, получим:
их выражениями, получим:

Сделав подстановку значений т1, т2, 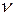 , R и
, R и 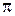 , найдем линейную скорость человека:
, найдем линейную скорость человека:
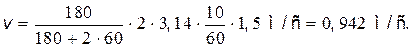
Дата добавления: 2015-02-10; просмотров: 619; Мы поможем в написании вашей работы!; Нарушение авторских прав |