
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач 3 страница

 Пример 18. Человек стоит в центре скамьи Жуковского и вместе с ней вращается по инерции. Частота вращения
Пример 18. Человек стоит в центре скамьи Жуковского и вместе с ней вращается по инерции. Частота вращения 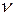 1=0,5 c-1. Момент инерции jo тела человека относительно оси вращения равен 1,6 кг·м2. В вытянутых в стороны руках человек держит по гире массой m=2 кг каждая. Расстояние между гирями l1=l,6 м. Определить частоту вращения
1=0,5 c-1. Момент инерции jo тела человека относительно оси вращения равен 1,6 кг·м2. В вытянутых в стороны руках человек держит по гире массой m=2 кг каждая. Расстояние между гирями l1=l,6 м. Определить частоту вращения 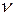 2, скамьи с человеком, когда он опустит руки и расстояние l2 между гирями станет равным 0,4 м. Моментом инерции скамьи пренебречь.
2, скамьи с человеком, когда он опустит руки и расстояние l2 между гирями станет равным 0,4 м. Моментом инерции скамьи пренебречь.
Решение. Человек, держащий гири (рис. 12), составляет вместе со скамьей замкнутую механическую систему, поэтому момент импульса J  этой системы должен иметь постоянное значение. Следовательно, для данного случая
этой системы должен иметь постоянное значение. Следовательно, для данного случая
J1  = J2
= J2  ,
,
где J и  — момент инерции тела человека и угловая скорость скамьи и человека с вытянутыми руками; J2 и
— момент инерции тела человека и угловая скорость скамьи и человека с вытянутыми руками; J2 и  — момент инерции тела человека и угловая скорость скамьи и человека с опущенными руками. Отсюда:
— момент инерции тела человека и угловая скорость скамьи и человека с опущенными руками. Отсюда:
 = (J1/J2)
= (J1/J2)  .
.
Выразив в этом уравнении угловые скорости  и
и  через частоты вращения
через частоты вращения 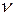 1 и
1 и 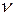 2 (
2 (  =2
=2 
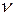 ) и сократив на 2
) и сократив на 2  , получим:
, получим:
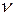 2=(J1/J2)
2=(J1/J2) 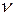 1. (1)
1. (1)
Момент инерции системы, рассматриваемой в данной задаче, равен сумме момента инерции тела человека J0 и момента инерции гирь в руках человека. Так как размер гирь много меньше расстояния их от оси вращения, то момент инерции гирь можно определить по формуле момента инерции материальной точки: J=mr2. Следовательно,
J1=J0+2m(l1/2)2;

|
где т — масса каждой из гирь; l1 и l2. — первоначальное и конечное расстояние между гирями. Подставив выражения J1 и J2 в уравнение (1), получим:
 . (2)
. (2)
Выполнив вычисления по формуле (2), найдем
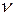 2=1,18 с-1.
2=1,18 с-1.
Пример 19. Стержень длиной l=1,5 м и массой М=10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня (рис. 13). В середину стержня ударяет пуля массой m=10 г, летящая в горизонтальном направлении со скоростью vo=500 м/с, и застревает в стержне. На какой угол  отклонится стержень после удара?
отклонится стержень после удара?
Решение. Удар пули следует рассматривать как неупругий: после удара и пуля, и соответствующая точка стержня будут двигаться с одинаковыми скоростями.
 Рассмотрим подробнее явления, происходящие при ударе. Сначала пуля, ударившись о стержень, за ничтожно малый промежуток времени приводит его в движение с угловой скоростью
Рассмотрим подробнее явления, происходящие при ударе. Сначала пуля, ударившись о стержень, за ничтожно малый промежуток времени приводит его в движение с угловой скоростью  и сообщает ему кинетическую энергию
и сообщает ему кинетическую энергию
 (1)
(1)
где  — момент инерции стержня относительно оси вращения.
— момент инерции стержня относительно оси вращения.
Затем стержень поворачивается на искомый угол  , причем центр масс его поднимается на высоту
, причем центр масс его поднимается на высоту  . В отклоненном положении стержень будет обладать потенциальной энергией
. В отклоненном положении стержень будет обладать потенциальной энергией
 (2)
(2)
Потенциальная энергия получена за счет кинетической энергии и равна ей по закону сохранения энергии. Приравняв правые части равенств (1) и (2), получим
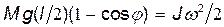
Отсюда
 .
.
Подставив в эту формулу выражение для момента инерции стержня  , получим
, получим
 (3)
(3)
Чтобы из выражения (3) найти  , необходимо предварительно определить значение
, необходимо предварительно определить значение  . В момент удара на пулю и на стержень действуют силы тяжести, линии действия которых проходят через ось вращения и направлены вертикально вниз. Моменты этих сил относительно оси вращения равны нулю. Поэтому при ударе пули о стержень будет справедлив закон сохранения момента импульса. В начальный момент удара угловая скорость стержня
. В момент удара на пулю и на стержень действуют силы тяжести, линии действия которых проходят через ось вращения и направлены вертикально вниз. Моменты этих сил относительно оси вращения равны нулю. Поэтому при ударе пули о стержень будет справедлив закон сохранения момента импульса. В начальный момент удара угловая скорость стержня  , поэтому его момент импульса
, поэтому его момент импульса  . Пуля коснулась стержня и начала углубляться в стержень, сообщая ему угловое ускорение и участвуя во вращении стержня около оси. Начальный момент импульса пули
. Пуля коснулась стержня и начала углубляться в стержень, сообщая ему угловое ускорение и участвуя во вращении стержня около оси. Начальный момент импульса пули  , где
, где  — расстояние точки попадания от оси вращения. В конечный момент удара стержень имел угловую скорость
— расстояние точки попадания от оси вращения. В конечный момент удара стержень имел угловую скорость  , а пуля — линейную скорость
, а пуля — линейную скорость  , равную линейной скорости точек стержня, находящихся на расстоянии
, равную линейной скорости точек стержня, находящихся на расстоянии  от оси вращения. Так как
от оси вращения. Так как  , то конечный момент импульса пули
, то конечный момент импульса пули  .
.
Применив закон сохранения импульса, можем написать:
 , или
, или  ,
,
откуда:
 , (4)
, (4)
где  — момент инерции стержня.
— момент инерции стержня.
Если учесть, что в (4)  , а также что
, а также что  , то после несложных преобразований получим:
, то после несложных преобразований получим:
 (5)
(5)
Подставив числовые значения величин в (5), найдем
 рад = 0,5 рад.
рад = 0,5 рад.
По (3) получим:

Следовательно,  =9°20'
=9°20'
Пример 20. Из пружинного пистолета был произведен выстрел вертикально вверх. Определить высоту h, на которую поднимается пуля массой m = 20 г, если пружина жесткостью k = 196 Н/м была сжата перед выстрелом на х = 10 см. Массой пружины пренебречь.
Решение. Система пуля — Земля (вместе с пистолетом) является замкнутой системой, в которой действуют консервативные силы — силы упругости и силы тяготения. Поэтому для решения задачи можно применить закон сохранения энергии в механике. Согласно этому закону, полная механическая энергия  системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии
системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии  в конечном состоянии (когда пуля поднялась на высоту h), т. е.
в конечном состоянии (когда пуля поднялась на высоту h), т. е.
 =
=  , или
, или  , (1)
, (1)
где  и
и  — кинетические энергии системы в начальном и конечном состояниях;
— кинетические энергии системы в начальном и конечном состояниях;  и
и  — потенциальные энергии в тех же состояниях.
— потенциальные энергии в тех же состояниях.
Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид
 =
=  . (2)
. (2)
Если потенциальную энергию в поле тяготения Земли на ее поверхность принять равной нулю, то энергия системы в начальном состоянии равна потенциальной энергии сжатой пружины, т. е.
 , а в конечном состоянии — потенциальной энергий пули на высоте
, а в конечном состоянии — потенциальной энергий пули на высоте 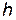 , т. е.
, т. е.  .
.
Подставив приведенные выражения  и
и  в формулу (2), найдем
в формулу (2), найдем
 ;
;  .
.
Произведя вычисления по последней формуле, получим h=5 м.
Пример 21. Точка совершает колебания по закону  , где А=2 см. Определить начальную фазу φ, если
, где А=2 см. Определить начальную фазу φ, если
x(0)=  см и
см и  (0)<0. Построить векторную диаграмму для момента t=0.
(0)<0. Построить векторную диаграмму для момента t=0.
Решение. Воспользуемся уравнением движения и выразим смещение в момент t=0 через начальную фазу:
 .
.
Отсюда найдем начальную фазу:
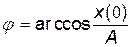 .
.
Подставим в это выражение заданные значения x(0) и А: 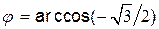 . Значению аргумента
. Значению аргумента  удовлетворяют два значения угла:
удовлетворяют два значения угла:

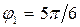 и
и  .
.
Для того чтобы решить, какое из этих значений угла φ удовлетворяет еще и условию 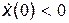 , найдем сначала
, найдем сначала 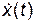 :
:
 .
.
 Подставив в это выражение значение t=0 и поочередно значения начальных фаз
Подставив в это выражение значение t=0 и поочередно значения начальных фаз 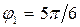 и
и  , найдем:
, найдем:
 ;
;  .
.
Так как всегда A>0 и ω>0, то условию 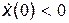 удовлетворяет только первое значение начальной фазы. Таким образом, искомая начальная фаза
удовлетворяет только первое значение начальной фазы. Таким образом, искомая начальная фаза 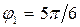 .
.
По найденному значению φ построим векторную диаграмму (рис. 14).
Пример 22. Материальная точка массой m=5 г совершает гармонические колебания с частотой ν =0,5 Гц. Амплитуда колебаний A=3 см. Определить: 1) скорость v точки в момент времени, когда смещение х= 1,5 см; 2) максимальную силу Fmax, действующую на точку; 3) полную энергию 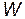 колеблющейся точки.
колеблющейся точки.
Решение. 1. Уравнение гармонического колебания имеет вид:
 , (1)
, (1)
а формулу скорости получим, взяв первую производную по времени от смещения:
 (2)
(2)
Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого возведем оба уравнения в квадрат, разделим первое на  , второе на
, второе на  и сложим:
и сложим:
 или
или  .
.
Решив последнее уравнение относительно  , найдем
, найдем
 .
.
Выполнив вычисления по этой формуле, получим
 см/с.
см/с.
Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус — когда направление скорости совпадает с отрицательным направлением оси х.
Смещение при гармоническом колебании кроме уравнения (1) может быть определено также уравнением:
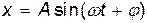 .
.
Повторив с этим уравнением такое же решение, получим тот же ответ.
2. Силу, действующую на точку, найдем по второму закону Ньютона:
 (3)
(3)
где а — ускорение точки, которое получим, взяв производную по времени от скорости:
 , или
, или 
Подставив выражение ускорения в формулу (3), получим:
 .
.
Отсюда максимальное значение силы:
 .
.
Подставив в это уравнение значения величин π, ν, m и A, найдем:
 мН.
мН.
3. Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени.
Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигает максимального значения. В этот момент потенциальная энергия равна нулю. Поэтому полная энергия 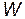 колеблющейся точки равна максимальной кинетической энергии
колеблющейся точки равна максимальной кинетической энергии  max:
max:
 (4)
(4)
Максимальную скорость определим из формулы (2), положив  ;
;  . Подставив выражение скорости в формулу (4), найдем
. Подставив выражение скорости в формулу (4), найдем

Подставив значения величин в эту формулу и произведя вычисления, получим
 Дж = 22,1·10-6Дж или
Дж = 22,1·10-6Дж или 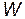 =22,1 мкДж.
=22,1 мкДж.
Пример 23. На концах тонкого стержня длиной l = 1 м и массой m3=400 г укреплены шарики малых размеров массами m1=200 г и m2=300г. Стержень колеблется около горизонтальной оси, перпендикулярной стержню и проходящей через его середину (точка О на рис. 15). Определить период Т колебаний, совершаемых стержнем.
Решение. Период колебаний физического маятника, каким является стержень с шариками, определяется соотношением

 (1)
(1)
где J — момент инерции маятника относительно оси колебаний; m – его масса; lС — расстояние от центра масс маятника до оси.
Момент инерции данного маятника равен сумме моментов инерции шариков J1 и J2 и стержня J3:
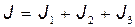 (2)
(2)
Принимая шарики за материальные точки, выразим моменты их инерции:  ;
; 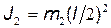 .
.
 Так как ось проходит через середину стержня, то его момент инерции относительно этой оси
Так как ось проходит через середину стержня, то его момент инерции относительно этой оси 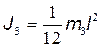 . Подставив полученные выражения J1 , J2 и J3 в формулу (2), найдем общий момент инерции физического маятника:
. Подставив полученные выражения J1 , J2 и J3 в формулу (2), найдем общий момент инерции физического маятника:
 .
.
Произведя вычисления по этой формуле, найдем  кг·м2.
кг·м2.
Масса маятника состоит из масс шариков и массы стержня:
 =0,9 кг.
=0,9 кг.
Расстояние lС центра масс маятника от оси колебаний найдем, исходя из следующих соображений. Если ось х направить вдоль стержня и начало координат совместить с точкой О, то искомое расстояние l равно координате центра масс маятника, т. е.
 .
.
Подставив значения величин m1, m2, m, l и произведя вычисления, найдем:
 см.
см.
Произведя расчеты по формуле (1), получим период колебаний физического маятника:
 с = 11,2 с.
с = 11,2 с.
Пример 24.Складываются два колебания одинакового направления, выражаемых уравнениями  ;
;  , где А1=1см, A2=2 см,
, где А1=1см, A2=2 см,  с,
с,  с, ω =
с, ω =  с-1. 1. Определить начальные фазы φ1 и φ2 составляющих колебаний. 2. Найти амплитуду А и начальную фазу φ результирующего колебания. Написать уравнение результирующего колебания.
с-1. 1. Определить начальные фазы φ1 и φ2 составляющих колебаний. 2. Найти амплитуду А и начальную фазу φ результирующего колебания. Написать уравнение результирующего колебания.
Решение. 1. Уравнение гармонического колебания имеет вид
 (1)
(1)
Преобразуем уравнения, заданные в условии задачи, к такому же виду:
 ,
,  (2)
(2)
Из сравнения выражений (2) с равенством (1) находим начальные фазы первого и второго колебаний:
 рад и
рад и  рад.
рад.
 2. Для определения амплитуды А результирующего колебания удобно воспользоваться векторной диаграммой, представленной на рис. 16. Согласно теореме косинусов, получим
2. Для определения амплитуды А результирующего колебания удобно воспользоваться векторной диаграммой, представленной на рис. 16. Согласно теореме косинусов, получим
 , (3)
, (3)
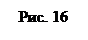 где
где  — разность фаз составляющих колебаний. Так как
— разность фаз составляющих колебаний. Так как  , то, подставляя найденные значения φ2 и φ1 получим
, то, подставляя найденные значения φ2 и φ1 получим 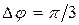 рад.
рад.
Подставим значения А1 , А2и  в формулу (3) и произведем вычисления:
в формулу (3) и произведем вычисления:
A=2,65 см.
Тангенс начальной фазы φ результирующего колебания определим непосредственно из рис. 16: 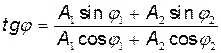 , откуда начальная фаза
, откуда начальная фаза
 .
.
Подставим значения А1, А2, φ1, φ2 и произведем вычисления:
 рад.
рад.
Так как угловые частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту ω. Это позволяет написать уравнение результирующего колебания в виде  , где A=2,65 см, ω =
, где A=2,65 см, ω =  с-1,
с-1,  рад.
рад.
Пример 25.Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых
 , (1)
, (1)
 , (2)
, (2)
где А1=1 см, A2=2 см, ω =  с-1. Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
с-1. Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
Решение. Чтобы найти уравнение траектории точки, исключим время t из заданных уравнений (1) и (2). Для этого воспользуемся формулой  . В данном случае
. В данном случае  , поэтому
, поэтому 
Так как согласно формуле (1)  , то уравнение траектории
, то уравнение траектории
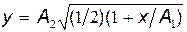 (3)
(3)
Полученное выражение представляет собой уравнение параболы, ось которой совпадает с осью Ох. Из уравнений (1) и (2) следует, что смещение точки по осям координат ограничено и заключено в пределах от – 1 до +1 см по оси Ох и от – 2 до +2 см по оси Оу.
 Для построения траектории найдем по уравнению (3) значения у, соответствующие ряду значений х, удовлетворяющих условию
Для построения траектории найдем по уравнению (3) значения у, соответствующие ряду значений х, удовлетворяющих условию  см, и составим таблицу:
см, и составим таблицу:
| x,см | – 1 | – 0,75 | – 0,5 | +0,5 | + 1 | |
| у,см | ±0,707 | ±1 | ±1,41 | ±1,73 | ±2 |
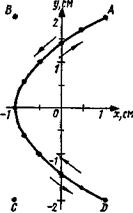
Начертив координатные оси и выбрав масштаб, нанесем на плоскость хОу найденные точки. Соединив их плавной кривой, получим траекторию точки, совершающей колебания в соответствии с уравнениями движения (1) и (2) (рис. 17).
 Для того чтобы указать направление движения точки, проследим за тем, как изменяется ее положение с течением времени. В начальный момент t=0 координаты точки равны x(0)=1 см и y(0)=2 см. В последующий момент времени, например при t1=l с, координаты точек изменятся и станут равными х(1)= – 1 см, y(1)=0. Зная положения точек в начальный и последующий (близкий) моменты времени, можно указать направление движения точки по траектории. На рис. 17 это направление движения указано стрелкой (от точки А к началу координат). После того как в момент t2 = 2 с колеблющаяся точка достигнет точки D, она будет двигаться в обратном направлении.
Для того чтобы указать направление движения точки, проследим за тем, как изменяется ее положение с течением времени. В начальный момент t=0 координаты точки равны x(0)=1 см и y(0)=2 см. В последующий момент времени, например при t1=l с, координаты точек изменятся и станут равными х(1)= – 1 см, y(1)=0. Зная положения точек в начальный и последующий (близкий) моменты времени, можно указать направление движения точки по траектории. На рис. 17 это направление движения указано стрелкой (от точки А к началу координат). После того как в момент t2 = 2 с колеблющаяся точка достигнет точки D, она будет двигаться в обратном направлении.
Дата добавления: 2015-02-10; просмотров: 723; Мы поможем в написании вашей работы!; Нарушение авторских прав |