Примеры решения задач 4 страница

Пример 26. Космический корабль движется со скоростью =0,9с по направлению к центру Земли. Какое расстояние l пройдет этот корабль в системе отсчета, связанной с Землей (K-система), за интервал времени Δt₀=1 с, отсчитанный по часам, находящимся в космическом корабле (K'-система)? Суточным вращением Земли и ее орбитальным движением вокруг Солнца пренебречь.

Решение. Расстояние l, которое пройдет космический корабль в системе отсчета, связанной с Землей (K-система), определим по формуле

(1)

где — интервал времени, отсчитанный в K-системе отсчета. Этот интервал времени связан с интервалом времени, отсчитанным в K'-системе, соотношением .

Подставив выражение в формулу (1), получим:

После вычислений найдем:

l=619 Мм.

Пример 27.В лабораторной системе отсчета (K-система) движется стержень со скоростью =0,8с.По измерениям, произведенным в K-системе, его длина l оказалась равной 10 м, а угол φ, который он составляет с осью х, оказался равным 30° . Определить собственную длину l₀ стержня в K'-системе, связанной со стержнем, и угол φ₀, который он составляет с осью х' (рис. 18)

Решение. Пусть в K'-системе стержень лежит в плоскости х'О'у'. Из (рис. 18, а) следует, что собственная длина l₀ стержня и угол φ₀, который он составляет с осью х', выразятся равенствами

(1)

В K-системе те же величины окажутся равными (рис. 18, б)

(2)

Заметим, что при переходе от системы К' к К размеры стержня в направлении оси у не изменятся, а в направлении оси х претерпят релятивистское (лоренцево) сокращение, т. е.

, (3)

С учетом последних соотношений собственная длина стержня выразится равенством

или

Заменив в этом выражении на (рис. 18, б), получим

Подставив значения величин в это выражение и произведя вычисления, найдем

l₀=15,3 м.

Для определения угла воспользуемся соотношениями (1), (2) и (3):

, или

откуда

.

Подставив значения φ и β в это выражение и произведя вычисления, получим

.

Пример 28.Кинетическая энергия Т электрона равна 1 МэВ. Определить скорость электрона.

Решение. Релятивистская формула кинетической энергии

Выполнив относительно β преобразования, найдем скорость частицы, выраженную в долях скорости света ( ):

(1)

где E₀= =0,511 МэВ — энергия покоя электрона.

Вычисления по этой формуле можно производить в любых единицах энергии, так как наименования единиц в правой части формул сократятся и в результате подсчета будет получено отвлеченное число.

Подставив числовые значения Е₀и Т в мегаэлектрон-вольтах, получим

β=0,941.

Так как , то

м/с.

Чтобы определить, является ли частица с кинетической энергией Т релятивистской или классической, достаточно сравнить кинетическую энергию частицы с ее энергией покоя.

Если , частицу можно считать классической. В этом случае релятивистская формула (1) переходит в классическую:

, или .

Пример 29. Определить релятивистский импульс р и кинетическую энергию Т электрона, движущегося со скоростью (где с — скорость света в вакууме).

Решение. Релятивистский импульс

(1)

После вычисления по формуле (1) получим

кг·м/с.

В релятивистской механике кинетическая энергия Т частицы

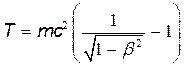. (2)

Сделав вычисления, найдем

T=106 фДж.

Во внесистемных единицах энергия покоя электрона =0,511 МэВ. Подставив это значение в формулу (2), получим

Т=0,66 МэВ.

Пример 30.Релятивистская частица с кинетической энергией (m – масса частицы) испытывает неупругое столкновение с такой же покоящейся (в лабораторной системе отсчета) частицей. При этом образуется составная частица. Определить: 1) массу составной частицы; 2) ее кинетическую энергию Т'.

Решение. 1. Для того чтобы найти массу составной частицы, воспользуемся инвариантностью величины

. (1)

До столкновения (в лабораторной системе отсчета):

полная энергия частиц ,

импульс частиц ,

.

После столкновения (в системе отсчета связанной с составной частицей):

энергия и импульс составной частицы ,

.

В силу инвариантности величины (1) .

Тогда масса составной частицы:

.

2. Скорость составной частицы (равна скорости центра масс частиц до столкновения) .

Кинетическая энергия составной релятивистской частицы:

.

Таблица вариантов