
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 8. Предел функции.
8.1. Вычислить предел функции при х  х
х  :
:
В-1. f(x) =  а) х
а) х  = 2; б) х
= 2; б) х  = -1; в) х
= -1; в) х  =
=  .
.
Вариант 2. f(x) =  а) х
а) х  = -1; б) х
= -1; б) х  = 1; в) х
= 1; в) х  =
=  .
.
Вариант 3. f(x) = 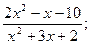 а) х
а) х  = 2; б) х
= 2; б) х  = -2; в) х
= -2; в) х  =
=  .
.
Вариант 4. f(x) =  а) х
а) х  = 1; б) х
= 1; б) х  = 2; в) х
= 2; в) х  =
=  .
.
Вариант 5. f(x) =  а) х
а) х  = -2; б) х
= -2; б) х  = -1; в) х
= -1; в) х  =
=  .
.
Вариант 6. f(x) =  а) х
а) х  = -1; б) х
= -1; б) х  = 1; в) х
= 1; в) х  =
=  .
.
Вариант 7. f(x) =  а) х
а) х  = 2; б) х
= 2; б) х  = -3; в) х
= -3; в) х  =
=  .
.
Вариант 8. f(x) = 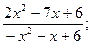 а) х
а) х  = 1; б) х
= 1; б) х  = 2; в) х
= 2; в) х  =
=  .
.
Вариант 9. f(x) = 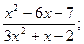 а) х
а) х  = -2; б) х
= -2; б) х  = -1; в) х
= -1; в) х  =
=  .
.
Вариант 10. f(x) =  а) х
а) х  = -1; б) х
= -1; б) х  = 1; в) х
= 1; в) х  =
=  .
.
8.2. Вычислить предел функции при х  х
х  :
:
В-1. f(x) = 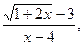 х
х  = 4. В-2. f(x) =
= 4. В-2. f(x) =  х
х  = -8. В-3. f(x) =
= -8. В-3. f(x) =  х
х  = 3. В-4. f(x) =
= 3. В-4. f(x) =  х
х  = 8. В-5. f(x) =
= 8. В-5. f(x) =  х
х  = -3. В-6. f(x) =
= -3. В-6. f(x) =  х
х  = 9.
= 9.
В-7. f(x) =  х
х  = 4. В-8. f(x) =
= 4. В-8. f(x) =  х
х  = -3.
= -3.
В-9. f(x) =  х
х  = -3. В-10. f(x) =
= -3. В-10. f(x) =  х
х  = 2.
= 2.
8.3. Вычислить предел функции при х  0:
0:
В-1. f(x) =  В-2. f(x) =
В-2. f(x) =  В-3. f(x) =
В-3. f(x) = 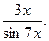 В-4. f(x) =
В-4. f(x) =  В-5. f(x) =
В-5. f(x) = 
В-6. f(x) =  В-7. f(x) = 3x·ctg5x. В-8. f(x) = 4x·ctg6x В-9. f(x) = x·ctg3x. В-10. f(x) =
В-7. f(x) = 3x·ctg5x. В-8. f(x) = 4x·ctg6x В-9. f(x) = x·ctg3x. В-10. f(x) = 
8.4. Вычислить предел функции при х 
 :
:
В -1. f (x) =  В - 2. f (x) =
В - 2. f (x) =  В-3. f (x) =
В-3. f (x) =  В - 4. f (x) =
В - 4. f (x) = 
В -5. f (x) =  В- 6. f (x) =
В- 6. f (x) =  В-7.f (x) =
В-7.f (x) =  В-8. f (x) =
В-8. f (x) = 
В -9. f (x) =  В - 10. f (x) =
В - 10. f (x) = 
Задание 9. Найти производные функций:
В – 1.а)у =  , б) у =
, б) у =  , в) у = sin 3x · e
, в) у = sin 3x · e  , г) y = arctg ln 2x.
, г) y = arctg ln 2x.
В – 2.а)у =  , б) у =
, б) у =  , в) у = ctg 4x · e
, в) у = ctg 4x · e  , г) y = sin
, г) y = sin  .
.
В – 3.а)у =  , б) у =
, б) у =  , в) у = cjsx · 3
, в) у = cjsx · 3  , г) y = ln
, г) y = ln  .
.
В – 4.а)у =  , б) у =
, б) у = 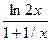 , в) у = tg 2x ·2
, в) у = tg 2x ·2  , г) y = ln
, г) y = ln  sinx.
sinx.
В – 5.а)у = 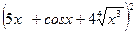 , б) у =
, б) у =  , в) у = arctgx ·(x
, в) у = arctgx ·(x  , г) y = e
, г) y = e  .
.
В – 6.а)у =  , б) у =
, б) у =  , в) у = cos 3x · e
, в) у = cos 3x · e  , г) y = ln arctg2x.
, г) y = ln arctg2x.
В –7.а)у =  б) у =
б) у = 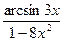 , у = tg2x · 2
, у = tg2x · 2  , г) y = cos ln 5x.
, г) y = cos ln 5x.
В – 8.а)у =  , б) у =
, б) у =  , в) у = ln2x · e
, в) у = ln2x · e  , г) y = cos
, г) y = cos  .
.
В – 9.а)у =  , б) у =
, б) у = 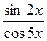 , у = sin 4x · e
, у = sin 4x · e  , г) y = arcsin ln 4x.
, г) y = arcsin ln 4x.
В – 10.а)у =  , б) у =
, б) у =  , в) у = tg 3x · 2
, в) у = tg 3x · 2  , г) y = sin ln 5x.
, г) y = sin ln 5x.
Задание 10. Найти вторую производную  от функции, заданной параметрически.
от функции, заданной параметрически.
Вариант 1.  Вариант 2.
Вариант 2.  Вариант 3.
Вариант 3. 
Вариант 4.  Вариант 5.
Вариант 5.  Вариант 6.
Вариант 6. 
Вариант 7.  Вариант 8.
Вариант 8.  Вариант 9.
Вариант 9.  Вариант 10.
Вариант 10. 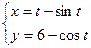
Дата добавления: 2015-02-10; просмотров: 226; Мы поможем в написании вашей работы!; Нарушение авторских прав |