Задание 11. Применение производной.

а) Составить уравнения касательной и нормали к графику кривой у = f(x) в точке, с абсциссой х₀.

Б) Найти максимальную скорость, если точка движется по закону S(t).

в) Найти наибольшее и наименьшее значения функции y = f(x) на [а; b].

Вариант 1. Вариант 2. Вариант 3.

а) у = -х² + 2х +3, x₀ = 1 а) у = 2х² - 3х +6, x₀ = -1 а) у = 2х² - 5х -3, x₀ = 2

б) S(t) = -1/6 t³+ 2t² + 3t + 5 б) S(t) = - t³+ 6t² + 24t - 5 б) S(t) = -1/3 t³+ 8t² - 8t – 5

в) f(x) = x³ – 6x² + 9x – 3 в) f(x) = 1/3x³ – x² + 6 в) f(x) =- x³ + 3x² + 2

на [0; 5]. на [-3; 2] на [1; 4].

Вариант 4. Вариант 5. Вариант 6.

а) у = - 1/2х² + 3х - 1, x₀ = 2 а) у = 1/2х² - 4х +2, x₀ = -2 а) у = 3х² - 7х + 2, x₀ = 1

б) S(t) = -1/3 t³+ 3t² + 15 б) S(t) = -1/6 t³+ 2t² + 4t – 7 б) S(t) = -1/6 t³+ 4t² + 5

в) f(x) = x³ –12x² +16 в) f(x) = x³ - 3x + 5 в) f(x) = -x³ +27x + 4

на [1; 7] на [-2; 4]. на [0; 4]

Вариант 7. Вариант 8.

а) у = -1/2х² + 3х +1/2, x₀ = -1 а) у = 1/2х² + 5х + 3, x₀ = 0

б) S(t) = - t³+ 24t² – 5 б) S(t) = -1/6 t³+ 1/2t² + 1/2t + 1

в) f(x) = x³ + 3x + 3 в) f(x) = -1/3x³ + x² - 1

на [-3; 2]. на [0; 3]

Вариант 9. Вариант 10.

а) у = -1/2х² + 3х +1/2, x₀ = -1 а) у = 1/2х² + 5х + 3, x₀ = 0

б) S(t) = - t³+ 24t² – 5 б) S(t) = -1/6 t³+ 1/2t² + 1/2t + 1

в) f(x) = x³ + 3x + 3 в) f(x) = -1/3x³ + x² - 1

на [-3; 2]. на [0; 3]

Задание 12. ИССЛЕДОВАНИЕ ФУНКЦИИ. Исследовать данные функции методом дифференциального исчисления и построить их графики.

Вариант 1. Вариант 2. Вариант 3.

а) у = 2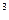х - 3х -12х –1 а) у 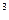= - х + 6х + 9х + 1 а) у = х 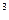-3х² – 9х +10

б) у = б) у = б) у =

Вариант 4. Вариант 5. Вариант 6.

а) у 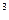= -х +9х -24х +12 а) у 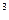= х + 3х -9х - 10 а) у = -х 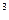+3х + 9х-10

б) у = б) у = б) у =

Вариант 7. Вариант 8. Вариант 9. Вариант 10.

а) у = 2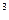х -3х -12х +5 а) у = -1/3х 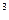+х +6 а) у = х 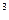- 12х + 5 а) у = х 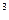+3х +2

б) у = б) у = б) у = б) у =