
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 16. Дифференциальное и интегральное исчисление функций нескольких переменных.
16.1Найти область определения функции и изобразить ее:
В-1.  В-2.
В-2.  В-3.
В-3. 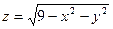 В-4.
В-4. 
В-5.  В-6.
В-6.  В-7.
В-7.  В-8.
В-8. 
В-9.  В-10.
В-10. 
16.2Дана функция z = f(x;y). Найти: 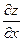 ,
,  ,
,  ,
,  ,
,  :
:
В-1.z =  В-2.z =
В-2.z =  В-3.z =
В-3.z =  В-4.z =
В-4.z = 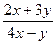 В-5.z =
В-5.z = 
В-6.z =  В-7.z =
В-7.z =  В-8.z =
В-8.z =  В-9.z =
В-9.z =  В-10.z =
В-10.z = 
16.3.Дана функция z = f(x;y), точка М( х  ; y
; y  ) и вектор
) и вектор  = {х
= {х  ;у
;у  }. Найти:
}. Найти:
а) производную в точке М по направлению вектора  ; б) grad z в точке М.
; б) grad z в точке М.
В-1. z = у2 + х2 +2xy- у; М( 1; 1) и вектор  = {2;-1}. В-2. z = x –y + 3y2 + x2; М( 1; 2) и вектор
= {2;-1}. В-2. z = x –y + 3y2 + x2; М( 1; 2) и вектор  = {5;-12}.
= {5;-12}.
В-3. z = x 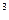 - y3 – 3xy; М( 1; 1) и вектор
- y3 – 3xy; М( 1; 1) и вектор  = {2;1}. В-4.z = xy – x2y – xy2; М( -1; 2) и вектор
= {2;1}. В-4.z = xy – x2y – xy2; М( -1; 2) и вектор  = {4;-3}.
= {4;-3}.
В-5. z = y2 – x2 + xy - 2x - 6y; М( 2; 3) и вектор  = {4;-3}. В-6.z = 6xy + 5x2 ; М( 2; 1) и вектор
= {4;-3}. В-6.z = 6xy + 5x2 ; М( 2; 1) и вектор  = {1;2}.
= {1;2}.
В-7.z = ln (5x2 + 3y2); М( 1; 1) и вектор  = {3;2}. В-8.z = у2 - х2 +xy; М( 1; 1) и вектор
= {3;2}. В-8.z = у2 - х2 +xy; М( 1; 1) и вектор  = {2;-1}.
= {2;-1}.
В-9.z = x 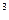 +8y3 – 6xy + 1; М( 1; 2) и вектор
+8y3 – 6xy + 1; М( 1; 2) и вектор  = {5;-12}. В-10.z = ln (3x2 + 4y2); М( 1; 3) и вектор
= {5;-12}. В-10.z = ln (3x2 + 4y2); М( 1; 3) и вектор  = {2;-1}
= {2;-1}
16.4.Найти точки экстремума функции:
В-1.f(x) = x2 +xy + y2 + x +2y – 4 В-2.f(x) =-3 x2 - 2xy - 3 y2 - 12x +12y – 25
В-3.f(x) =- 2 x2 - xy - 2 y2 - 2 x - 8y -54 В-4.f(x) = 2x2 + 2xy +2 y2 +2 x + 4y -3
В-5.f(x) = - x2 - 2xy - 3 y2 - 4 x -4y + 3В-6.f(x) = 3x2 + 3xy +3 y2 +6 x + 3y + 1
В-7.f(x) =- 3x2 - 2xy - y2 - 4 x - 4y + 3 В-8.f(x) = - x2 - 2xy - 3y2 - 6x - 6y + 5
В-9. f(x) = 2x2 + 2xy + 2y2 + 6x + 6y + 1 В-10. f(x) = - x2 - xy - y2 - 3x - 3y + 2
16.4.Составить уравнение касательной плоскости и нормали к поверхности в точке С(х  ;y
;y  ;z
;z  ):
):
В-1.z = xy – x2y – xy2 , С(1;2;z  )
)  В-2.z = x –y + 3y2 + x2 ; С(-1;2;z
В-2.z = x –y + 3y2 + x2 ; С(-1;2;z  )
)
В-3.z = y2 + x2 - 9xy + 27, С(2;1;z  )
) 
 В-4.z = 3x + 6y –xy + y2 –x2, С(1;-1;z
В-4.z = 3x + 6y –xy + y2 –x2, С(1;-1;z  )
) 
В-5.z = 2xy + 3y2 – 5x; С(3;4;z  ) В-6.z = x
) В-6.z = x  - y
- y  +5x +4y ; С(2;3;z
+5x +4y ; С(2;3;z  )
)
В-7.z = x  + y
+ y  +2x +y - 1; С(2;4;z
+2x +y - 1; С(2;4;z  ) В-8.z = xy + 2y
) В-8.z = xy + 2y  - 2x; С(1;2;z
- 2x; С(1;2;z  )
)
В-9.z = x  + 3xy - 6y; С(1;3;z
+ 3xy - 6y; С(1;3;z  )
)  В-10.z = x
В-10.z = x  - y
- y  +6x +3y; С(2;3;z
+6x +3y; С(2;3;z  )
) 
Задание 17. Дифференциальные уравнения.
17.1. Найти общее решение линейного уравнения первого порядка:
В.1 а)  ; б)
; б)  . В.2 а)
. В.2 а)  ; б)
; б) 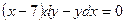
В.3 а)  ; б)
; б)  . В.4 а)
. В.4 а)  б)
б) 
В.5 а)  ; б)
; б)  . В.6 а)
. В.6 а) 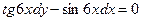 б)
б) 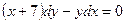
В.7 а)  ; б)
; б)  . В.8 а)
. В.8 а)  б)
б) 
В.9 а)  ; б)
; б)  . В.10 а)
. В.10 а)  б)
б) 
17.2.Найти общее решение:
В.1а) у²+4у¢ -12у = 0 б) у² -10у¢+25у =0 в) у² -2у¢+5у = 0
В.2а) у² -7у¢ = 0 б) у²+16у¢+64у=0 в) у² -8у¢+ 25у =0
В.3а)у²+5у¢+6у =0 б) у²+14у¢+49у =0 в) у²+4у¢+7у = 0
В.4а)у² -4у = 0 б) у²+4у¢+4у =0 в) у²+2у¢+5у = 0
В.5а)у² -7у¢ -8у = 0 б) у²+2у¢+2у = 0 в)у²+6у¢+9у = 0
В.6а)у²-у¢ -6у =0 б) у² -18у¢+81у =0 в) у²+2у¢+2у = 0
В.7а) у² -5у¢ = 0 б) у²-16у¢+64у=0 в) у² -8у¢+ 25у =0
В.8а)у²-4у¢ -12у = 0 б) у² +10у¢+25у =0 в) у² -2у¢+5у = 0
В.9а) у² +7у¢ -8у = 0 б) у²+2у¢+2у = 0 в) у²+6у¢+9у = 0
В.10а) у²+у¢ -6у =0 б) у² +18у¢+81у =0 в) у²+2у¢+2у = 0
17.3.Найти частное решение:
В.1 у² -3у¢+2у = 0, если у = 2, у¢ = 3,при х = 0 В.2у²+у¢ -6у = 0, если у = 3, у¢ = 1 при х = 0
В.3у² -2у¢ -8у = 0, если у=4, у¢= 10, при х =0 В.4у² -3у¢ = 0, если у =1, у¢= -1, при х = 0
В.5у²+у¢ -6у = 0, если у = 0, у¢ = -10 при х=0 В.6у² -3у¢+2у = 0, если у =1, у¢=3 при х =0
В.7у²+2у¢ -8у = 0, если у =4, у¢= -4 при х =0 В.8у² +3у¢ = 0, если у =1, у¢= -1, при х = 0
В.9у²- у¢ -6у = 0, если у = 0, у¢ = -10 при х=0 В.10у² -3у¢+2у = 0, если у =2, у¢=3 при х =0
Дата добавления: 2015-02-10; просмотров: 265; Мы поможем в написании вашей работы!; Нарушение авторских прав |