
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 13.Интеграл.
1. Найти неопределенный интеграл, проверить результат дифференцированием в заданиях а, б,в,г.
2. Вычислить неопределенный интеграл в заданиях д,е.
3. Вычислить определенный интеграл в задании ж.
Вариант 1. а)  б)
б)  в)
в) 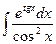 г)
г) 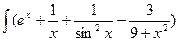 dx д)
dx д)  е)
е)  ж)
ж) 
Вариант 2. а) 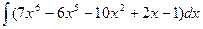 б)
б) 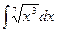 в)
в) 
г)  д)
д)  е)
е)  ж)
ж) 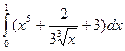
Вариант 3. а)  б)
б)  в)
в)  г)
г)  д)
д)  е)
е) 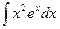 ж)
ж) 
Вариант 4. а)  б)
б) 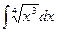 в)
в) 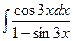 г)
г)  д)
д)  е)
е)  ж)
ж) 
Вариант 5. а)  б)
б) 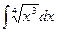 в)
в)  г)
г)  д)
д)  е)
е) 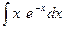 ж)
ж) 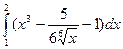
Вариант 6. а)  б) 5/3
б) 5/3  в)
в)  г)
г) 
д) 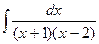 е)
е)  ж)
ж) 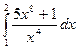
Вариант 7. а) 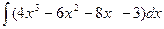 б)14
б)14  в)
в)  г)
г)  д)
д)  е)
е)  ж)
ж) 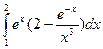
Вариант 8. а)  б) 8
б) 8  в)
в)  г)
г)  д)
д) 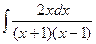 е)
е) 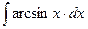 ж)
ж) 
Вариант 9. а)  б) 11
б) 11 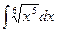 в)
в)  г)
г)  д)
д) 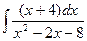 е)
е)  ж)
ж) 
Вариант 10. а)  б) 7
б) 7  в)
в)  г)
г) 
д) 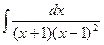 е)
е) 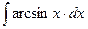 ж)
ж) 
Задание 14. Площадь фигуры.
С помощью определенного интеграла вычислить площадь фигуры, ограниченной линиями. Сделать чертеж.
Вариант 1. Вариант 2.
а) х + у – 3 = 0, 2х – у + 6 = 0, у = 0. а) х + у –6 = 0, х – у +4 = 0, у = 0.
б) у = х2, у = 2х + 3. б) у = х2, у = 4х - 3.
Вариант 3. Вариант 4.
а) х - 2у + 4 = 0, х + 2у - 8 = 0, у = 0. а) х - у +3 = 0, х + у -1 = 0, у = 0.
б) у = х2, у = -2х + 3. б) у = х2, у = -4х - 3.
Вариант 5. Вариант 6.
а) 3х + 7у – 18 = 0, 3х – 2у + 9 = 0, у = 0. а) 2х + у –12 = 0, 4х – 7у +12 = 0, у = 0.
б) 3х2 –4у = 0, 2х – 4у + 1 = 0. б) 3х2 + 4у = 0, 2х – 4у- 1 = 0.
Вариант 7. Вариант 8.
а) 2х - 3у + 2 = 0, 2х + у - 10 = 0, у = 0. а) х - у +2 = 0, 3х + 4у -15 = 0, у = 0.
б) 3х2 - 4у = 0, 2х + 4у – 1 = 0. б) 3х2 – 2у = 0, 2х – 2у + 1 = 0.
Вариант 9. Вариант 10.
а) 3х + 4у – 15 = 0, 3х – 2у + 3 = 0, у = 0. а) 4х + 5у –16 = 0, 4х – 2у +16 = 0, у = 0.
б) 3х2 –2у = 0, 2х + 2у - 1 = 0. б) у = 3х2 + 1, у = 3х +7.
Задание 15. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Вычислить приближенное значение определенного интеграла с помощью формулы Симпсона, разбив отрезок на 10 частей, с точностью до 0,001
В.1 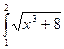 dx В.2
dx В.2  dx В.3
dx В.3  dx В.4
dx В.4  В.5
В.5  В.6
В.6  В.7
В.7 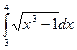 В.8
В.8  dx В.9
dx В.9 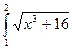 dx В.10
dx В.10  dx
dx
Дата добавления: 2015-02-10; просмотров: 248; Мы поможем в написании вашей работы!; Нарушение авторских прав |