Среднее линейное отклонение взвешенное

Показывает на сколько в среднем каждая варианта отклоняется от средней величины.

Для определения минимальной величины отклонения вместо средней величины может быть использована медиана:

Среднее линейное отклонение выражается в тех же единицах, что и отдельные значения признака.

Дисперсия представляет собой средний квадрат отклонения отдельных значений признака от их средней величины

Рассчитать дисперсию можно так же по преобразованной формуле:

где - средний квадрат значений признака в совокупности:

- квадрат среднего значения признака в совокупности.

При расчете дисперсии по этой формуле исключается дополнительная процедура по расчету отклонений индивидуальных значений признака от его средней величины, за счет этого уменьшается ошибка, связанная с округлением значений промежуточных вычислений.

Среднее квадратическое отклонение – это корень из дисперсии

_пр = - простое

_вз = - взвешенное

Среднее квадратическое отклонение измеряется в тех же единицах, что и значение признака. Широко применяется при проведении выборочных наблюдений для определения ошибок выборки и границ вариации признака.

Среднее квадратитческое отклонение всегда больше по величине среднего линейного отклонения.

Для оценки интенсивности вариации, а также для сравнения ее величины в разных совокупностях или по разным признакам используют относительные показатели вариации, которые рассчитываются как отношение абсолютных показателей вариации к средней величине признака. Чаще всего они выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. Различают следующие относительные показатели вариации:

Коэффициент осцилляции:

Линейный коэффициент вариации: =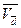

Коэффициент вариации: =

Чем меньше коэффициент вариации, тем однороднее совокупность.

Пример: имеются данные о группе предприятий по стоимости основных фондов

Группировка предприятий по стоимости основных фондов, млн. руб.	Число предприятий f	Середина интервала «Х»			Х2	Х2f
4-6 6-8 8-10 10-12 12-14			9,4 8,1 3,5 7,8 13,2	44,18 21,87 2,45 10,14 43,56
				122,2