Нормальное распределение

Исключительно важную роль в теории вероятностей играет нормальное распределение (закон Гаусса).

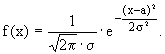Непрерывная случайная величина  имеет нормальное распределение вероятностей с параметрами а,  > 0, если плотность распределения ее имеет вид:

Нормальный закон распределения широко применяется в практических задачах, он проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину  влияет незначительно.

Функция распределения такой случайной величины имеет вид:

то есть M = a.

D =  ² .

Таким образом, параметры а,  ² в выражении есть математическое ожидание и дисперсия нормально распределенной случайной величины, а

График плотности вероятности имеет вид нормальной кривой (Гаусса):

Отметим некоторые свойства нормальной кривой.

1. Кривая распределения симметрична относительно прямой х = а.

2.

3.

4. При изменении математического ожидания и при  = Const, происходит смещение кривой вдоль оси Ох. Если положить а = Const и изменять  , то кривая изменяет свой вид в зависимости от  .

Рис. 14.4

Пусть  - нормальная случайная величина с параметрами (0,1), Тогда ее плотность имеет вид:

,

а функция распределения

Если взять , то получим, независимо от а,

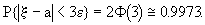
Формула носит название правила трех сигм.