КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Экспоненциальное (показательное) распределение
В практических приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике, биологии, теории надежности, часто имеют дело со случайными величинами, которые имеют экспоненциальное распределение.
Случайная величина распределена по показательному закону с параметром >0, если она непрерывна и имеет следующую плотность распределения вероятностей:
(14.7)
Тогда
(x > 0).
Таким образом,
(14.6)
соответственно, графики f(x) и F(x) имеют вид:
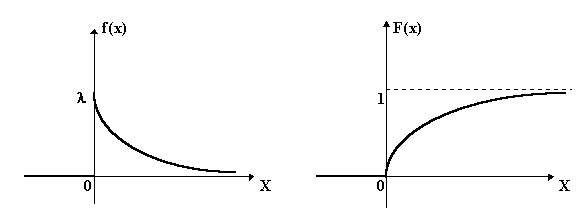
Определим числовые характеристики:
Распределение Пирсона
С начала ХХ века оказался очень полезным введенный Пирсоном закон c 2 (рис.2): в страховом деле, в выяснении торгового спроса или популярности политиков и т.п.
Рис.2. Плотность распределения вероятностей закона c 2, с n степенями свободы.
Под аргументом х здесь понимается сумма n независимых слагаемых в квадрате, каждое из которых подчиняется нормальному Z- закону с m =0 и s =1. Ясно, что при больших n (практически при n >30) закон c 2 превращается в нормальный закон с m = n и s = 
, поскольку действует теорема Ляпунова. Но чаще всего слагаемых не более 10. Число n называеся числом степеней свободы. Смысл f(x) такой же, как и в нормальном законе: вероятность числовой величине х=c 2 попасть в заданный диапазон равна площади под кривой f(x). Так, площадь под кривой на отрезке от 0 до n + составляет более 90% всей площади под всей кривой f(x). Отсюда следут правило “трех s “ для закона c 2: с вероятностью рі 0,9 случайная величина х=c 2 не превосходит величины n +Ц 2n (очевидно, c 2 не может быть отрицательным).
Распределение Стьюдента
Наконец, необходимо упомянуть закон t Стьюдента, полученный из нормального закона и закона c 2. Случайная величина t получается из дроби в числителе которой стоит случайная величина Z Гаусса с m=0 и s =1, а в знаменателе - случайная величина c 2 с n степенями свободы. По -прежнему при больших n закон Стьюдента переходит в нормальный закон (практически при n і 30). Но даже при небольших n вид кривой плотности распределения вероятностей для t очень похож на кривую 3 рис.1. Разница в том, что вместо s =1 для Z необходимо брать s =n /(n -2), т.е.среднее отклонение t от m=0 больше, чем среднее отклонение Z от m=0. Соответственно “холм” закона t более пологий, чем “холм” закона Z.
Это распределение связано с нормальным. Если СВ x1, x2, … xn – независимы, и каждая из них имеет стандартное нормальное распределение N(0,1), то СВ имеет распределение, называемое распределением Стьюдента:
Дата добавления: 2015-02-10; просмотров: 137; Мы поможем в написании вашей работы!; Нарушение авторских прав |