Распределение Пуассона. Играет важную роль в ряде вопросов физики, теории связи, теории надежности, теории массового обслуживания и т.д

Играет важную роль в ряде вопросов физики, теории связи, теории надежности, теории массового обслуживания и т.д. Всюду, где в течение определенного времени может происходить случайное число каких-то событий (радиоактивных распадов, телефонных вызовов, отказов оборудования, несчастный случаях и т.п.).

Рассмотрим наиболее типичную ситуацию, в которой возникает распределение Пуассона. Пусть некоторые события (покупки в магазине) могут происходить в случайные моменты времени. Определим число появлений таких событий в промежутке времени от 0 до Т.

Случайное число событий, происшедших за время от 0 до Т, распределено по закону Пуассона с параметром l=аТ, где а>0 – параметр задачи, отражающий среднюю частоту событий. Вероятность k покупок в течение большого интервала времени, (например, – дня) составит

P(Z=k) =

Биномиальное распределение (распределение Бернулли)

Возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях.

Для удобства и наглядности будем полагать, что нам известна величина p – вероятность того, что вошедший в магазин посетитель окажется покупателем и (1– p) = q – вероятность того, что вошедший в магазин посетитель не окажется покупателем.

Если X – число покупателей из общего числа n посетителей, то вероятность того, что среди n посетителей оказалось k покупателей равна

P(X= k) = 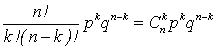, где k=0,1,…n

Формулу называют формулой Бернулли. При большом числе испытаний биномиальное распределение стремиться к нормальному.

Ситуация неопределенности значения параметра предполагает, что имеется информация только о границах диапазона возможного изменения параметра без информации о возможном распределении внутри этого диапазона; Ситуация моделируется заданием диапазона изменения неопределенной величины: для одной величины для системы

Кроме того, представляется совокупность неформализуемых сведений об условиях операции, обусловливающих границы диапазонов значений {γ}. Данные о диапазонах используются при моделировании непосредственно, а данные {γ} учитываются как при моделировании, так и при анализе результатов.

В настоящее время ситуация неопределенности значения находится в стадии разработки, что определяет неоднозначность способов ее задания*

При соответствующем уменьшении неопределенности значения данная ситуация может быть сведена к ситуации стохастичности.

Уменьшение неопределенности значения обусловлено:

- приданием диапазону значений параметра объективной вероятностной меры;

- изменением диапазона неопределенности;

- возрастанием субъективной вероятности попадания неопределенной величины в заданный диапазон;

- возрастанием объема сведений {γ}.

Уменьшение неопределенности значения связано с дополнительными мероприятиями при проведении анализа эффективности системы:

- использованием соответствующих технических решений по компонентам операции, позволяющих компенсировать неопределенности значения;

- привлечением (при возможности) дополнительной информации;

- «тренировкой» ЛПР для соответствующего проведения анализа полученных результатов моделирования.

При анализе неопределенных ситуаций различают неопределенные и ошибочные сведения. Ошибка не отождествляется с неопределенностью и устраняется; методы устранения ошибок достаточно разработаны и их изложение выходит за рамки настоящего материала.

Ситуация неопределенности значения может рассматриваться как предельный случай неопределенности параметра.

Неопределенности значений в наибольшей степени связаны с прогнозированием параметров, описывающих:

- условия первой группы в части реакции противостоящей системы, стратегии и тактики использования ее средств противодействия;

- определяющий комплекс условий модели операции второй группы в части условий проведения операции, определяемых противостоящей системой (например, периода проведения ЛА ответных действий);

- реакции суперсистемы, определяемые большим числом разнородных факторов*

Ситуация_неопределенности параметра предполагает отсутствие какой-либо информации о значениях моделируемого параметра при наличии некоторых неформализуемых сведений {γ} по условиям операции в части данного параметра.

В модели операции ситуация неопределенности параметра непосредственно не формализуется. Однако на этапе анализа полученных результатов моделирования объем сведений {γ} предполагает формирование допущений в части соответствующего параметра, принятых при моделировании.

При уменьшении неопределенности параметра эту ситуацию можно свести к ситуации неопределенности значения. Уменьшение неопределенности параметра осуществляется за счет возрастания объема сведений {γ} и получения дополнительный сведений о возможных значениях параметра.

При проведении анализа эффективности элемента СТС уменьшение неопределенности параметра связано с системой следующих мероприятий:

- привлечение дополнительной информации (по возможности) за счет проведения экспертных оценок и натурного эксперимента;

- соответствующая подготовка ЛПР для проведения анализа результатов моделирования,

Следует отметить, что ситуация неопределенности параметра характерна для первых итераций анализа; при последующих итерациях эта ситуация либо исключается, либо сводится к ситуации неопределенности значения. Особое значение для изучения этой ситуации имеет метод экспертных оценок, Ситуацию неопределенности параметра следует отличать от ситуации ошибочных сведений: ошибочные сведения не отождествляются с неопределенностью и должны быть исключены. Ситуация неопределенности параметра в определенных условиях может рассматриваться как частный случай ситуации неосведомленности.

Ситуация неосведомленности предполагает отсутствие в модели операции искомого параметра, который в реальном процессе имеет значение (влияет на исход операции). Ситуация неосведомленности неформализуема и не рассматривается в модели операции, обусловливая ошибку моделирования.

Ситуация неосведомленности характерна для таких явлений, как будущие открытия по компонентам моделирования, появление информации о ранее не известных процессах, взаимодействие средств в реальных условиях и т.д. Исключение ситуации неосведомленности осуществляется только на основе проведения натурных экспериментов. Однако на этапе анализа эффективности проектируемых ЛА возможности по проведению таких экспериментов крайне ограничены, если не исключены вовсе. Поэтому ЛПР должно учитывать возможность возникновения ситуации неосведомленности и пути ее компенсации.

К основным принципам исключения ситуации неосведомленности можно отнести:

- проведение соответствующего анализа по принимаемым новым, ранее не опробованным техническим решениям;

- наличие перераспределяемых технических ресурсов для компенсации ситуации в случае ее возникновения;

- постановку натурных экспериментов по компонентам модели (при наличии возможности) на всех этапах ее разработки и использования*