
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Представление функции в виде полинома Жегалкина
1. Представим любую функцию формулой над {x1&x2, 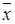 } и сделаем замену
} и сделаем замену 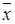 =xÅ1. Этот способ удобен, если функция задана формулой.
=xÅ1. Этот способ удобен, если функция задана формулой.
Пример 2. (x1 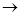 (x2
(x2 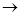 x3))(x1 Ú x2) x3 = (x1Ú x2 Ú x3)(x1 Ú x2) x3 = (`x1x2 Ú x1x3 Ú x1x2 Ú x2 Ú x2x3)x3 = (`x1x3 Ú x2)x3 = x1x3 x2 x3 = ((x1x3Å1)x2Å1)x3 = x1x2x3Åx2x3Åx3.
x3))(x1 Ú x2) x3 = (x1Ú x2 Ú x3)(x1 Ú x2) x3 = (`x1x2 Ú x1x3 Ú x1x2 Ú x2 Ú x2x3)x3 = (`x1x3 Ú x2)x3 = x1x3 x2 x3 = ((x1x3Å1)x2Å1)x3 = x1x2x3Åx2x3Åx3.
Надо помнить, что четное число одинаковых слагаемых в сумме по mod2 дает 0.
2. Метод неопределенных коэффициентов. Он удобен, если функция задана таблицей.
Пример 3. Запишем с неопределенными коэффициентами полином Жегалкина для функции трех переменных f(x1, x2, x3) = (01101001) = а0 Å а1х1Å Å а2х2 Å а3х3 Å b1x1x2 Å b2x2x3 Å b3x1x3 Å cx1x2x3. Затем находим коэффициенты, используя значения функции на всех наборах. На наборе (0, 0, 0) f(0, 0, 0) = 0, с другой стороны, подставив этот набор в полином, получим f(0, 0, 0) = а0, отсюда а0 = 0. f(0, 0, 1) = 1, подставив набор (0, 0, 1) в полином, получим: f(0, 0, 1) = а0 Å а3, т.к. а0 = 0, отсюда а3 = 1. Аналогично, f(0, 1, 0) = 1 = а2, f(0, 1, 1) = 0 = а2 Å а3 Å b2 = b2 = 0; а1 = 1; 0 = а1 Å а3 Å b3 = b3 = 0; 0 = а1 Å а2 Å b1 = b1 = 0; 1 = 1 Å 1 Å 1 Å c; c = 0; f(x1, x2, x3) = x1 Å x2 Å x3.
3. Многочлен Жегалкина можно получить также с помощью треугольника Паскаля по единицам его левой стороны по таблице следующим образом. Построим многочлен Жегалкина для функции f = (10011110). Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать шесть слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответсвует набору (101). В качестве слагаемого многочлена берем x1x3. Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
| N | x1x2x3 | f | Треугольник Паскаля | |||||
| x3 x2 x2x3 x1 x1x3 x1x2 x1x2x3 | 1 0 0 1 1 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 1 0 | |||||||
Тогда 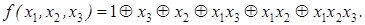
Дата добавления: 2014-11-13; просмотров: 428; Мы поможем в написании вашей работы!; Нарушение авторских прав |