
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сравнение валового дохода и валовых издержек.
В деятельности конкурентной фирмы различают краткосрочный и долгосрочный периоды. Автором «долгих» и «коротких» периодов является А. Маршалл. Во П томе «Принципов экономической науки» он пишет: «Для коротких периодов парк средств производства практически постоянен, но его использование колеблется в зависимости от спроса». (Маршалл А. Принципы экономической науки.- С. 60). «В долгие периоды динамика объёма средств производства приспосабливается к спросу на продукцию этих средств производства (там же.- С. 64).
Целью всякой фирмы в современной экономике является максимизация прибыли.
П = TR – TC, (10.1)
где П – прибыль,
TR – валовой доход,
TC – валовые издержки
TR=pQ, (10.2.)
где р – цена,
Q – объём реализованной продукции
Таким образом,
П=pQ – TC (10.3)
Исходя из наших рассуждения, величина прибыли зависит от цены, объёма и валовых издержек. Цена в условиях совершенной конкуренции не зависит от деятельности конкурентной фирмы и не является фактором, которым можно управлять. Это внешнее условие деятельности фирмы, которая в совершенно конкурентном рынке является ценополучателем. Валовые издержки также во многом зависят от объёма выпускаемой продукции. Таким образом, главным фактором, от которого зависит объём прибыли для совершенно конкурентной фирмы выступает количество выпускаемой продукции. Для определения оптимального количества продукции существует два способа:
1. Сравнение валового дохода(TR) и валовых издержек (TC);
2. Сравнение предельного дохода(MR) и предельных издержек(MC).
При этом возможны три принципиальных варианта поведения фирмы:
· Производство ради максимизации прибыли
· Производство ради минимизации убытков
· Прекращение производства
Рассмотрим перечисленные варианты более подробно.
1. Сравнение TR и ТС.
а) Случай максимизации прибыли. Допустим, на продукцию фирмы установился высокий уровень цены р1 в 5 денежных единиц, тогда
| Q | TR |
Табличным данным соответствует следующий график:

Рис. 10.3. Сравнение TR и ТС (случай максимизации прибыли).
Любой объём производства на участке QоQ2 принесёт фирме прибыль, но только при условии выпуска Q1 единиц продукта прибыль достигнет своего максимального значения.
Таким образом, конкурентная фирма выберет объём производства Q1 единиц продукции, при котором разность (TR – TC) максимальна.
б) Случай минимизации убытков. Допустим, что на продукцию фирмы установился некий средний уровень цены р2, равный 3 денежным единицам, тогда
| Q | TR |
График будет иметь следующую форму:
р
TC

 VC TR
VC TR



 Q
Q
Q0
Рис. 10.4. Сравнение TR и ТС (случай минимизации убытков).
В результате сравнения валового дохода и валовых издержек TR оказался меньше ТС. Фирма терпит убытки. Но она не закроется. Существует правило: если TR > VC, фирма будет продолжать производство, т.к. полученный доход TR позволяет покрывать все переменные издержки (VC) и даже часть постоянных издержек (FC). В данном случае перед фирмой стоит задача минимизации убытков. Эта задача решается в точке Q0, когда разность (TR –TC) минимальна.
в) Случай закрытия. Допустим. На продукцию фирмы установился низкий уровень цен р3, равный 1 денежной единице, тогда
| Q | TR |
Перенесём табличные данные на график:
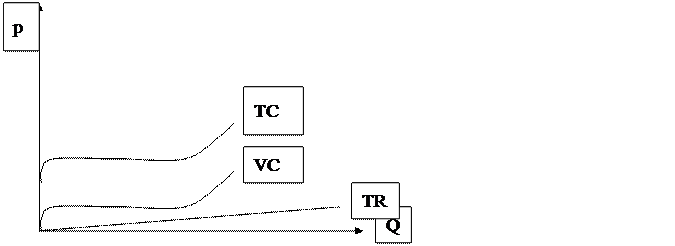
Рис.10.5. Сравнение TR и ТС (случай закрытия)
В результате сравнения оказалось, что валовые издержки больше валового дохода. Причём переменные издержки также больше, чем валовой доход. В этом случае фирма прекратит своё производство.
3. Сравнение предельного дохода и предельных издержек.
Более точным способом определения оптимального объёма производства является сравнение предельного дохода (MR) и предельных издержек (MC). По аналогии с валовым доходом и валовыми издержками рассмотрим три возможных случая: максимизации прибыли, минимизации убытков и закрытия.
а) Случай максимизации прибыли. Допустим, что на продукцию фирмы установился высокий уровень цен р1, равный 5 денежным единицам, тогда
| Q | MR=TRn -TRn-1 |
| 5=5–0 | |
| 5=10–5 | |
| 5=15–10 |
Данные таблицы изобразим графически:
 p
p
MC
 ATC
ATC
 MR
MR

 Q1 Q
Q1 Q
Рис. 10.6. Сравнение MR и МС (случай максимизации прибыли).
До тех пор, пока расширение производства будет обеспечивать превышение предельного дохода над предельными издержками фирма будет наращивать производство. Когда дополнительный объём производства приведёт к превышению предельных издержек над предельным доходом фирма прекратит расширять производство. Переломной точкой станет равенство MR и МС. Это точка максимизации совокупной прибыли фирмы при условии, что ATC < MR.
б) Случай минимизации убытков. Допустим. На рынке установлен средний уровень цен р2 3 денежных единицы., тогда
| Q | MR |
| 3=3–0 | |
 2 2
| 3=6–3 |
| 3=9–6 |
Графическое изображение:
 p
p
MC
 |
 ATC
ATC
AVC

 Q2 Q
Q2 Q
Рис. 10.7. Сравнение MR и МС (случай минимизации убытков)
В результате снижения цены предельный доход фирмы уменьшится и АТС окажутся больше, чем предельный доход. Существует правило: в случае ATC > MR фирме выгодно продолжать производство продукции, если MR > AVC, т.к. полученный доход позволит компенсировать все AVC и даже часть AFC (средних постоянных издержек). Точка Q2 соответствует точке минимизации убытков (это точка равенства MR и МС),
в) Случай закрытия. Предположим, что рынок установил цену на низком уровне р3 1 денежная единица, тогда
| Q | MR |
| 1=1–0 | |
| 1=2–1 | |
| 1=3–2 |
График будет иметь следующий вид:


 P ATC
P ATC
 AVC
AVC
MC
 |
 MR
MR
 Q3 Q
Q3 Q
Рис. 10.8. Сравнение MR и МС (случай закрытия).
Используя правило MR =МС, наиболее оптимальный объём производства находится в точке Q3. Однако в этом случае предельный доход не превышает не только АТС, но и AVC. Фирма не сможет компенсировать даже части своих AFC. Единственный выход в данном случае – прекратить производство.
Кривая предложения фирмы в краткосрочном периоде совпадёт с кривой МС при условии, что MR > AVC.
 |
 p S
p S
 Q
Q
Рис. 10.9. Кривая предложения совершенно конкурентной фирмы в краткосрочном периоде.
Дата добавления: 2014-11-13; просмотров: 1305; Мы поможем в написании вашей работы!; Нарушение авторских прав |