Типовые динамические звенья

Системы автоматического регулирования удобно представлять в виде соединения элементов, каждый из которых описывается алгебраическим или дифференциальным уравнением не выше второго порядка. При этом, одно и то же дифференциальное уравнение может описывать разные по своей физической природе элементы. Иными словами, у них одна математическая модель. Наиболее употребительные математические модели получили название типовых звеньев. Типовые звенья имеют одну входную и одну выходную величину.

Все конструктивное разнообразие САР можно представить небольшим числом типовых звеньев или их комбинаций.

Рассмотрим следующие типовые звенья.

Звенья, описываемые алгебраическими уравнениями:

- усилительное (пропорциональное),

- запаздывающее.

Звенья, описываемые дифференциальным уравнением первого порядка:

- инерционное,

- интегрирующее,

- дифференцирующее.

Звено, описываемое дифференциальным уравнением второго порядка. В зависимости от соотношения коэффициентов, оно может быть колебательнымили апериодическим.

Характеристики типовых звеньев принято указывать для единичного ступенчатого входного воздействия.

Для полной характеристики типового звена следует указать его дифференциальное уравнение, операторное уравнение, передаточную функцию, комплексную, действительную, мнимую, амплитудную, фазовую, логарифмическую амплитудную, логарифмическую фазовую частотные характеристики и переходную функцию.

1) Усилительное звено. y(t) = k x(t)

2) запаздывающее звено y(t) = kx(t - τ)

h(t)

k

0 t t

3) Инерционное звено ,

L(w)

L₂

L₁ 20lgk

0 lgw

4) Интегрирующее звено

5)Дифференцирующее звено .

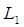
0

6)Колебательное звено ,

7) Апериодическое звено второго порядка