Действие вертикальной сосредоточенной силы, приложенной к поверхности линейно-деформируемого полупространства.

Рассмотрим действие сосредоточенной силы Р, приложенной перпендикулярно к ограничивающей полупространство плоскости (рис. 6.2). Будем считать полупространство однородным в глубину и в стороны и линейно деформируемым.

Рис. 6.2. Схема действия сосредоточенной силы.

Задача будет заключаться в определении всех составляющих напряжений: σ_z, σ_y, σ_x, τ_zy, τ_zx, τ_xy, а также перемещений w_z, w_y, w_x для любой точки полупространства, имеющей координаты z, у, х или R и β.

Поставленная задача для упругого (а следовательно, и любого линейно деформируемого) полупространства впервые была полностью решена проф. Ж. Буссинеском (1885), а определение напряжений для площадок, параллельных ограничивающей полупространство плоскости, - проф. В. Кирпичевым и Н.А. Цытовичем (1923 - 1934). Здесь мы ограничимся выводом только формул напряжений для площадок, параллельных ограничивающей плоскости, как наиболее часто используемых в расчетной практике, т. е. напряжений σ_z, τ_zy и τ_zx. Возьмем точку М (рис. 6.2), определяемую полярными координатами R и β, и определим нормальное напряжение σ_R, действующее по направлению радиуса R, а затем по формулам перехода - и все составляющие напряжения для площадки, проведенной через точку М, параллельно ограничивающей плоскости.

Для упрощения вывода (окончательный результат которого полностью совпадает с решением Буссинеска) примем как постулат, что напряжение σ_R пропорционально cosβ и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы R².

Следует отметить, что, как показано Проктором и Мораном на I Международном конгрессе по механике грунтов (1936), это положение может быть выведено строго и из закона Всемирного тяготения Ньютона.

Таким образом, полагаем

, (6.1)

где А - некоторый коэффициент, определяемый из условия равновесия.

Рис. 6.3. Схема радиальных напряжений при действии сосредоточенной силы

Для составления уравнения равновесия проведем полушаровое сечение с центром в точке приложения сосредоточенной силы (рис. 6.3). Напряжения, нормальные к полушаровой поверхности, определяются выражением (6.1) и будут изменяться от нуля у ограничивающей плоскости до максимума по оси Z, но для выделенного элементарного шарового пояса с центральным углом dβ могут приниматься постоянными.

Условие равновесия - сумма проекций всех сил на вертикальную ось равна нулю, т. е.

, (6.2)

где dF - поверхность элементарного шарового пояса, равная

. (6.3)

Подставляя выражение для dF и σ_R в уравнение (6.3), получим

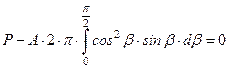. (6.4)

Произведя интегрирование и подставляя пределы, получим

, (6.5)

откуда неизвестный коэффициент пропорциональности

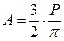. (6.6)

Подставляя полученное значение А в формулу (6.1), для радиальных напряжений будем иметь

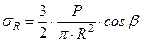. (6.7)

Отнесем величину радиальных напряжений не к площадке, перпендикулярной радиусу, а к площадке, параллельной ограничивающей плоскости и составляющей с ней угол β (рис. 6.4).

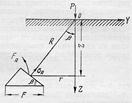
Рис. 6.4. Схема определения напряжений

Обозначим это напряжение .

Из геометрических соотношений находим, что , а так как , то

(6.8)

или, подставляя значение σ_R из выражения (6.7) и принимая во внимание, что , получим

. (6.9)

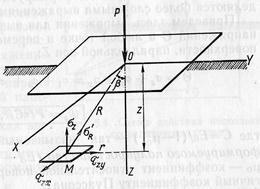
Рис. 6.5. Составляющие напряжений для площадки, параллельной ограничивающей плоскости.

Далее, не меняя направления площадки, разложим силу (рис. 6.5) на три направления: одно Z - перпендикулярное площадке и два X и У - лежащих в плоскости площадки. Тогда

. (6.10)

А так как ; ; , то величины составляющих для площадки, параллельной ограничивающей плоскости, окончательно будут иметь следующий вид:

. (6.11)

Отметим, что полученные выражения не содержат характеристик (модулей) деформируемости грунта, а, следовательно, справедливы для любых однородных грунтов. Составляющие же напряжений для вертикальных площадок будут зависеть от модуля деформации и коэффициента Пуассона. Приведём выражения составляющих напряжений для трёх взаимно-перпендикулярных площадок (рис. 6.6), а также для суммы главных напряжений θ и выражения для перемещений, параллельных осям координат. Составляющие напряжения будут равны:

Рис. 6.5. Схема составляющих напряжений.

Нормальные ; (6.12)

касательные ; (6.13)

сумма главных напряжений ; (6.14)

перемещения параллельно осям координат

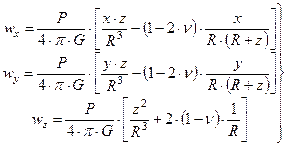. (6.15)

где - модуль сдвига,

- где x, y, z – координаты рассматриваемой точки.

Для многих вопросов механики грунтов особо важное значение имеют вертикальные составляющие напряжений и перемещения. Остановимся на них подробнее.

После преобразований можно записать следующее выражение для w_z

, (6.16)

где - коэффициент линейно-деформируемого полупространства.

Положение точки М на рис. 6.5 вполне определяется двумя её координатами z и r, где z – глубина от ограничивающей плоскости, r – расстояние от оси Z. Подставляя значение в выражение (6.12), получим

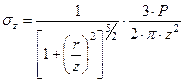или, обозначив

, (6.17)

получим

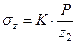(6.18)

Представляет также интерес решение для вертикальной погонной нагрузки Р в условиях плоской задачи (рис. 6.6), полученное Фламаном в 1892 г. в виде

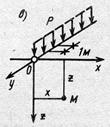
Рис. 6.6. Схема к задаче Фламана.

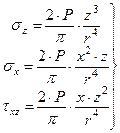(6.19)

где .

Зная закон распределения нагрузки на поверхности в пределах контура загружения, можно, интегрируя выражение (6.18) в пределах этого контура, определить значение напряжений в любой точке основания для случаев осесимметричной и пространственной нагрузки, а интегрируя выражение (6.19) – для случая полосовой нагрузки.