Определение напряжений методом угловых точек.

Приведенные выражения позволяют определить сжимающие напряжения в основании не только под центром или углом прямоугольной площадки загружения, но и по вертикали, проходящей через любую точку поверхности. Для этого применяется метод угловых точек. Здесь возможны три варианта решения (рис. 6.14).

Пусть вертикаль проходит через точку М, лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения σ_zM как сумму угловых напряжений I и II прямоугольников, т. е.

. (6.29)

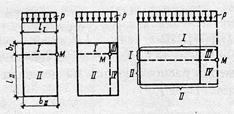
Рис. 6.14. Схема для расчёта напряжений методом угловых точек.

Соответственно значения напряжения и определяются по указанным выше правилам. Коэффициенты α^I и α^II находятся из табл. по значениям безразмерных параметров l_I/b_I, z/b_I и l_II/b_II, z/b_II, где, l_I, b_I, l_II, b_II - размеры сторон соответствующих прямоугольников. При этом всегда принимается, что .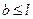

Если точка М лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника. Тогда

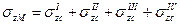. (6.30)

Наконец, если точка М лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой. Тогда, полагая, что напряжения в точке М возникают от действия нагрузки, распределенной по площади прямоугольников I и II, необходимо вычесть напряжения от действия той же фиктивной нагрузки, распределенной по площади прямоугольников III и IV, т. е. действительное напряжение определится выражением

. (6.31)

Естественно, что и в этих случаях правила определения угловых напряжений и соответствующих им значений коэффициентов α будут те же, что и приведенные для первого варианта.

Методом угловых точек обычно пользуются для расчетов взаимного влияния фундаментов, расположенных в непосредственной близости друг от друга.

Влияние формы и площади фундамента в плане.

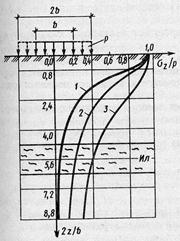Пользуясь формулой (6.28) и данными табл., можно построить эпюры нормальных напряжений σ_z по вертикальной оси, проходящей через центр прямоугольного фундамента. В качестве примера на рис. 6.15 в относительных координатах построены такие эпюры для случаев: 1 - квадратного фундамента при l=b; 2 - ленточного фундамента ( ) шириной b; 3 - то же, шириной 2b.

Рис. 6.15. Характер распределения напряжений σ_z по оси фундамента в зависимости от формы и площади его подошвы.

Легко заметить, что в случае пространственной задачи (кривая 1) напряжения с глубиной затухания значительно быстрее, чем для плоской задачи (кривая 2). Увеличение ширины, а, следовательно, и площади фундамента (кривая 3) приводит к еще более медленному затуханию напряжений с глубиной.

Это обстоятельство легко объяснить исходя из принципа суперпозиции. Представляя, например, ленточный фундамент как ряд квадратных фундаментов, установленных вплотную друг к другу, можно с помощью метода угловых точек учесть дополнительное влияние нагрузки, действующей на соседние фундаменты.

Указанная закономерность имеет важное практическое значение. Если, например, в основании на некоторой глубине залегает слабый прослоек (ил на рис. 6.15), то можно подобрать такую форму и площадь фундамента, чтобы напряжения на кровле этого прослойка были меньше его несущей способности. В противном случае возможны чрезмерные осадки из-за выдавливания грунта слабого прослойка в стороны от оси фундамента.