Действие нескольких сосредоточенных сил.

Если на поверхности изотропного линейно-деформируемого полупространства приложено несколько сосредоточенных сил Р₁, Р₂,…Р_n (рис. 6.8), то сжимающее напряжение в любой точке массива для горизонтальных площадок, параллельных ограничивающей плоскости, может быть найдено простым суммированием, используя принцип суперпозиции.

Рис. 6.8. Схема действия нескольких сосредоточенных сил.

, (6.22)

где К_i – коэффициенты, определяемые по формуле (6.17).

6.2.5. Действие любой распределённой нагрузки.

Используя приведенные выражения, можно достаточно просто с некоторым приближением определить напряжения в любой точке основания при любой форме фундамента и заданном законе распределения нагрузки. Поясним это на примере пространственной задачи.

Пусть на поверхности полупространства в пределах сложного контура действует некоторая распределенная нагрузка (рис. 6.9) Разбивая контур загружения на элементарные прямоугольники, заменим в пределах каждого прямоугольника распределенную нагрузку соответствующей силой .

Рис. 6.9. Схема к приближённому расчёту напряжений в любой точке основания.

Очевидно, что для элементов, прилегающих к контуру нагрузки, размеры площадей должны быть уточнены в соответствии с сеткой разбивки. Тогда от каждой силы P_i напряжение σ_zi в точке М, находящейся на глубине z от поверхности нагружения, определится по формуле (6.18), где . Очевидно, что для определения полного напряжения σ_z от действия всех элементарных сил необходимо выполнить суммирование по площади загружения.

Аналогичным образом, используя выражения (6.19), можно получить значения всех компонент напряжений для случая плоской задачи.

Точность решения зависит от размеров элементарных прямоугольников, на которые разбивается загруженный участок, и повышается с увеличением z. Если обозначить длинную сторону прямоугольника сетки разбиения Δy, то, как отмечает Н. А. Цытович, на глубине значение σ_z будет отличаться от полученного строгим решением на 6%, а на глубине - уже на 2%.

6.2.6. Действие равномерно распределённой нагрузки. Плоская задача

По мере увеличения отношения длины площади загружения l к ее ширине задача по определению напряжений все с большим основанием может рассматриваться как плоская (плоская деформация). При бесконечной длине полосы нагрузки l в каждом сечении, перпендикулярном ее продольной оси, будет одинаковая картина напряжений. Обычно рассматривают плоскую задачу, когда . В таком случае определяют три составляющих: нормальные напряжения σ_z, σ_x и касательные напряжения τ_xz. Указанные выше сечения остаются в процессе деформации плоскими (плоская деформация), следовательно, , а σ_y является функцией σ_z и σ_x.

Схема для расчета напряжений в основании в случае плоской задача при действии равномерно распределенной нагрузки интенсивностью р показана на рис. 6.10.

Рис. 6.10. Схема для расчёта напряжений в случае плоской задачи.

Для этого случая Г. В. Колосовым получены следующие точные выражения для определения компонент напряжений в любой точке упругого полупространства:

;

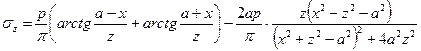; (6.23)

.

Если соотношения геометрических характеристик а, х, z в этих формулах представить в виде коэффициентов влияния К, то можно записать:

; ; .

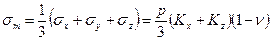. (6.24)

Коэффициенты влияния K_z, К_х, К_xz зависят от безразмерных параметров х/b и z/b, где х и z – координаты точки, в которой определяются напряжения, - ширина полосы загружения. Значения этих коэффициентов приведены в литературе.

Зная ширину фундамента b и задавшись координатами точки, в которой требуется определить напряжения, можно вычислить безразмерные параметры для этой точки и по данным таблицы определить соответствующие коэффициенты влияния. Затем при известной величине интенсивности нагрузки р по формулам (6. 24) нетрудно найти значения всех компонент напряжений в заданной точке.

Рассчитанные таким образом величины представлены на рис. 6.11 - в виде линий равных напряжений (изолиний напряжений). Видно, что по мере удаления от поверхности загружения интенсивность напряжений уменьшается и стремится к нулю. Вертикальные сжимающие напряжения σ_z распространяются преимущественно в глубь основания, горизонтальные сжимающие напряжения σ_x - в стороны от полосы загружения. Касательные напряжения τ_xz концентрируются по преимуществу под краями загруженной полосы.

Рис. 6.11. Линии равных напряжений (изобары) σ_z , (распоры) σ_x , (сдвиги) τ_xz при действии равномерно распределённой полосовой нагрузки.

Эпюры напряжений σ_z по вертикальным и горизонтальным сечениям при разных значениях y и z представлены на рис.6.12. Из рисунка видно, что в вертикальных сечениях напряжения σ_z с глубиной убывают, в горизонтальных сечениях они будут максимальными по оси полосовой нагрузки. Это свидетельствует о том, что напряжения с глубиной рассеиваются на всё большую площадь. В расчетах осадок широко используется эпюра напряжений σ_z, построенная по вертикальной оси, проходящей через центр площади фундамента.

Рис. 6.12. Эпюры напряжений σ_z по горизонтальным (ф) и вертикальным (б) сечениям.

Аналогичные решения получены и для других видов нагрузок (например, треугольной, параболической и т д.). Соответствующие коэффициенты влияния приведены в табличной форме в различных источниках (в частности, в учебниках Н. А. Цытовича по механике грунтов). Используя эти таблицы, можно самую сложную форму нагрузки представить как комбинацию простейших эпюр, Рассчитать в требуемой точке напряжения от каждой эпюры и, используя принцип суперпозиции, определить в этой точке суммарное напряжение от полной нагрузки.

В некоторых случаях при анализе напряженного состояния основания оказывается удобнее пользоваться главными напряжениями. Тогда значения главных напряжений в любой точке упругого полупространства под действием полосовой равномерно распределенной нагрузки можно определить по формулам И. X. Митчела:

, (6.25)

где α - угол видимости, образованный лучами, выходящими из данной точки к краям загруженной полосы (рис. 6.13). Эта формула позволяет не только определить значения главных напряжений, но и их ориентацию по отношению к осям х и z. Максимальное напряжение σ₁ действует по направлению биссектрисы угла видимости в данной точке, минимальное σ₃ - в перпендикулярном ему направлении. На рис. 6.13 для иллюстрации построены эллипсы напряжений, полуоси которых соответствуют значениям и направлению главных напряжений.

Рис. 6.13. Эллипсы напряжений при полосовой нагрузке.

6.2.7. Действие равномерно распределённой нагрузки. Пространственная задача.

Условия пространственного напряженного состояния в основании возникают тогда, когда по его поверхности действует местная нагрузка, распределенная по площади квадрата, прямоугольника, круга, эллипса и т. п. В этом случае неизвестными являются все компоненты напряжений. Для ряда таких задач имеются решения, полученные в замкнутом виде.

Значения вертикальных сжимающих напряжений σ_z в любой точке основания от действия нагрузки интенсивностью р, равномерно распределенной по площади прямоугольника размером , впервые были получены А. Лявом в 1935 г. Практический интерес представляют компоненты напряжений σ_zс, относящиеся к вертикали, проведенной через угловую точку С этого прямоугольника, и σ_z0, действующие по вертикали, проходящей через его центр (рис.6.13).

Рис. 6.13. Сжимающие напряжения под центром и под углом прямоугольника с равномерно распределённой нагрузкой.

Используя введенные выше понятия коэффициентов влияния, можно записать:

; , (6.26)

где K_zс и K_z0 - соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точка, в которой определяются напряжения.

Между значениями σ_zс и σ_z0 имеется определенное соотношение. Можно показать, что напряжения в точках, расположенных на вертикали, проходящей через центр площади загружения, равны учетверенным значениям угловых напряжений, действующих на удвоенной глубине, т. е.

. (6.27)

Тогда оказывается удобным выразить формулы (6.26) через общий коэффициент влияния α. и записать их в виде

; . (6.28)

Коэффициент α зависит от безразмерных параметров т и п. Параметр для обоих случаев является одинаковым. Следует помнить, что при определении углового напряжения σ_zс параметр m=z/b; при определении напряжения под центром прямоугольника σ_z0 параметр m=2z/b. Значения коэффициентов α приведены в табл.