Сила приложена внутри линейно-деформируемого полупространства.

Наряду с получившими широкое распространение в расчетах естественных оснований вышеприведённых решений, в ряде случаев (например, при анализе глубинного испытания грунтов пробными нагрузками, при исследовании работы свай и пр.) применяются формулы для определения напряжений от действия сосредоточенной силы, приложенной внутри линейно-деформируемого полупространства.

Для сосредоточенной силы Р, приложенной на глубине h и направленной перпендикулярно плоскости, ограничивающей линейно-деформируемое полупространство (рис. 6,7), составляющие напряжений и перемещений определяются по Р. Миндлину выражениями, значительно более сложными, чем для случая приложения силы на поверхности полупространства.

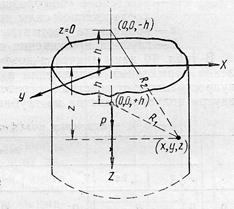
Рис. 6.7. Схема действия сосредоточенной силы внутри массива грунта.

Приведем здесь лишь формулы для вертикальных (параллельных оси Z) напряжений σ_z и перемещений W, имеющие наибольшее практическое приложение:

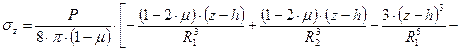
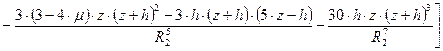; (6.20)

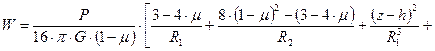
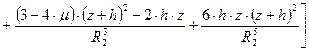, (6.21)

где ;

;

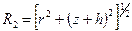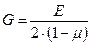- модуль сдвига;

Е - модуль деформации;

μ - коэффициент бркрвого расширения (аналогичный коэффициенту Пуассона);

z - координата рассматриваемой точки;

h - глубина приложения сосредоточенной силы.

Выражение (6.20) можно представить (по аналогии с выражением (6.18) в виде:

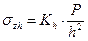, (6.21)

где K_h – безразмерный коэффициент, вычисляемый в зависимости от ординат z/h и r/h рассматриваемой точки, выраженных в долях от h (табулирован).