Область применения различных моделей.

Практика расчетов показывает, что модель местных упругих деформаций позволяет получить хорошее совпадение с действительностью при возведении фундаментов на сильносжимаемых грунтах (при МПа), на лёссовых просадочных грунтах, а также при ограниченной толще сжимаемых грунтов, подстилаемых практически недеформируемыми, например скальными, породами. Модель упругого полупространства применима при наличии в основании достаточно плотных грунтов и при не слишком больших площадях опорных поверхностей. Для сооружений с площадью опирания в десятки и сотни квадратных метров более близкие к действительности результаты дает модель упругого слоя ограниченной мощности.

6.3.5. Контактные напряжения на подошве центрально загруженных абсолютно жёстких фундаментов.

При определении контактных напряжений в этом случае исходят из того, что вертикальные перемещения любой точки поверхности грунта в уровне подошвы одинаковы, т. е. w(x, y)=const. Тогда для круглого в плане фундамента контактные напряжения определятся выражением

, (6.36)

где р_т - среднее напряжение под подошвой фундамента радиусом r

ρ - расстояние от центра фундамента до точки, в которой определяется ордината контактного напряжения р(ρ).

Аналогичным образом, определяются и контактные напряжения под жестким полосовым фундаментом в случае плоской задачи:

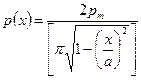, (6.37)

где х - расстояние от середины фундамента до рассматриваемой точки;

а = b/2- полуширина фундамента.

Приведенные решения показывают, что теоретически эпюра контактных напряжений под жестким фундаментом имеет седлообразный вид с бесконечно большими значениями напряжений по краям (при ρ = r или х = b/2). Однако вследствие пластических деформаций грунта в действительности контактные напряжения характеризуются более пологой кривой и у края фундамента достигают значений соответствующих предельной несущей способности грунта (пунктирная кривая на рис. 6.19, а).

Рис. 6.19. Эпюры контактных напряжений:

а) – под жёстким круглым штампом;

б) – под плоским фундаментом при различном показателе гибкости.

Изменение показателя гибкости существенно сказывается на изменении характера эпюры контактных напряжений. На рис. 6.19, б в качестве примера приведены контактные эпюры для случая плоской задачи при изменении показателя гибкости t от 0 (абсолютно жесткий фундамент) до 5.

Как отмечалось выше, достоверное знание контактных напряжений необходимо для расчетов конструкции фундаментов сооружений, взаимодействующих с грунтом. При расчетах напряжений в основаниях от действия нагрузок, соответствующих контактным напряжениям, часто оказывается возможным вводить существенные упрощения. Это связано с тем, что неравномерное распределение контактных напряжений по подошве фундамента оказывает заметное влияние на изменение напряжений лишь в верхней части основания на глубину порядка половины ширины фундамента.

6.3.6. Упрощённое определение контактных напряжений.

Если контактные напряжения по подошве фундамента определяются для последующих расчетов напряжений в основании, то допускается независимо от жесткости фундамента использовать формулы внецентренного сжатия. Тогда для центрально-нагруженного силой Р фундамента будет иметь место равномерное распределение напряжений по его подошве:

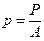, (6.38)

где А — площадь фундамента.

В случае плоской задачи при нагружении фундамента силой Р и моментом М, действующим в этой плоскости, краевые значения контактных напряжений определятся выражением

, (6.39)

где W — момент сопротивления площади подошвы выделенной полосы фундамента. Распределение контактных напряжений между этими значениями будет иметь линейный характер.

Теперь уже распределение напряжений в основании ниже подошвы фундамента можно рассчитать, если рассматривать полученную таким образом эпюру контактных напряжений как абсолютно гибкую местную нагрузку, действующую в этой плоскости.