
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Влияние неоднородности напластования грунтов.
Приведенные выше решения справедливы для случая, когда основание сложено грунтами, близкими по деформационным показателям. Если же на некоторой глубине залегают существенно более жесткие (например, скальные) грунты, возникает концентрация напряжений σz по оси фундамента, причем эффект концентрации напряжений тем больше, чем меньше относительная глубина залегания кровли этого слоя грунтов. Если же подстилающий слой грунта обладает значительно большей сжимаемостью, чем несущий, напротив, отмечается некоторое рассеивание (деконцентрация) напряжений σz.
На рис. 6.16 в качестве примера приведены также в относительных координатах эпюры напряжений σz по оси фундаментов.
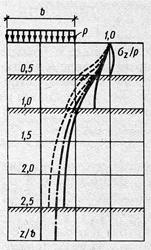
Рис. 6.16. Эпюры напряжений σz по оси фундамента при расположении подстилающего слоя на различной глубине:
-.-.-.- относительно однородное по сжимаемости основание;
____ при наличии на соответствующих относительных глубинах z/b практически несжимаемого слоя;
------ то же, но значительно более слабого слоя, чем несущий слой.
Определение напряжений по подошве фундаментов и сооружений.
Общие положения.
При взаимодействии фундаментов и сооружений с грунтами основания на поверхности контакта возникают контактные напряжения. Знание контактных напряжений необходимо как для расчета напряжений в основании, создаваемых сооружением, так и для расчетов самих конструкций.
Отметим, что расчет сооружений на действие контактных напряжений обычно рассматривается в курсе строительной механики.
Характер распределения контактных напряжений зависит от жёсткости, формы и размеров фундамента или сооружения и от жёсткости (податливости) грунтов основания. Различают три случая, отражающих способности сооружения и основания к совместной деформации:
1. абсолютно жесткие сооружения, когда деформируемость сооружения ничтожно мала по сравнению с деформируемостью основания, и при определении контактных напряжений сооружение можно рассматривать как недеформируемое;
2. абсолютно гибкие сооружения, когда деформируемость сооружения настолько велика, что оно свободно следует за деформациями основания;
3. сооружения конечной жесткости, когда деформируемость сооружения соизмерима с деформируемостью основания; в этом случае они деформируются совместно, что вызывает перераспределение контактных напряжений.
Характерными примерами абсолютно жестких конструкций являются массивные фундаменты под мостовые опоры, дымовые трубы, тяжелые прессы, кузнечные молоты и т. д., абсолютно гибких - земляные насыпи, днища металлических резервуаров и т. п. Большинство сооружений (плитные фундаменты, балки, ленточные фундаменты) по условиям работы конструкций имеют конечную жесткость.
Критерием оценки жесткости сооружения может служить показатель гибкости по М. И. Горбунову-Посадову
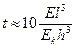 , (6.32)
, (6.32)
где Е и Ек - модули деформации грунта основания и материала конструкции; l и h - длина и толщина конструкции.
Конструкция сооружения или фундамента считается абсолютно жесткой, если 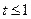 . В первом приближении жесткость конструкции можно оценить исходя из соотношения ее толщины и длины. При h/l > 1/3 конструкция может рассматриваться как абсолютно жесткая.
. В первом приближении жесткость конструкции можно оценить исходя из соотношения ее толщины и длины. При h/l > 1/3 конструкция может рассматриваться как абсолютно жесткая.
Существенное значение имеет также соотношение длины l и ширины b сооружения. При  распределение контактных напряжений соответствует случаю плоской задачи, при
распределение контактных напряжений соответствует случаю плоской задачи, при 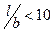 - пространственной.
- пространственной.
При определении контактных напряжений важную роль играет выбор расчетной модели основания и метода решения контактной задачи, причем расчетная модель основания часто бывает не связана собственно с моделью грунтов, слагающих массив, поэтому модели грунтового основания для расчетов контактных напряжений иногда называют контактными моделями.
Наибольшее распространение в инженерной практике получили следующие модели основания: местных упругих деформаций и упругого полупространства.
Основные предпосылки расчета контактных напряжений для случая плоской задачи заключаются в следующем. Из балки (рис. 6.17, а) вырезается полоса длиной 1м (рис. 6.17, б) и рассматривается распределение напряжений в разных точках контакта этой полосы ,с основанием по оси х. Принимается, что совместная деформация сооружения (полосы) и основания происходит без разрыва сплошности, т. е. в каждой точке контакта прогиб полосы и осадка основания равны и определяются величиной w(x).
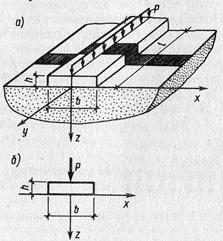
Рис. 6.17. Схема балки (а) и расчётная схема для случая плоской задачи (б).
Считая справедливой гипотезу плоских сечений, уравнение изогнутой оси полосы записывают в виде
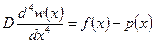 , (6.33)
, (6.33)
где 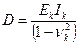 - цилиндрическая жесткость полосы;
- цилиндрическая жесткость полосы;
f(x) - интенсивность заданной на полосу нагрузки;
р(х) - интенсивность неизвестной эпюры контактных напряжений.
Напомним, что индекс «к» относится к конструкции; следовательно, Ек и νк - соответственно модуль упругости и коэффициент Пуассона материала полосы; Ik - момент инерции ее поперечного сечения.
В уравнении (6.33) содержатся две неизвестные величины: w(x) и р(х). Следовательно, для решения задачи необходимо введение дополнительного условия. Это условие определяется в зависимости от принятия той или иной модели: местных упругих деформаций или упругого полупространства.
Дата добавления: 2015-04-11; просмотров: 453; Мы поможем в написании вашей работы!; Нарушение авторских прав |