Обработка данных и получение статистических оценок

Для проведения мониторинга его участникам необходимо владеть основными методами статистической обработки материалов. Эти методы позволяют оценить точность и достоверность полученных результатов, избежать ошибочных выводов.

11.1.1. Оценка среднего значения и его погрешности

При наблюдениях или измерениях возникает необходимость установ­ления их точности (достоверности, насколько полученное среднее значе­ние отражает истинное значение измеряемой величины).

Рассмотрим конкретный пример. Допустим, что мы занимаемся изучением влияния загрязнений крупного завода на прирост сосны. Предположим, что мы измерили прирост в высоту 100 сосен и получили следующие значения в сантиметрах:

34, 26, 30, 43, 33, 37, 22, 28, 35, 39, 30, 30, 29, 42, 34, 43, 32, 29, 38, 35, 36, 42, 26, 36, 35, 38, 38, 38, 38, 34, 36, 44, 36, 40, 34, 22, 41, 40, 53, 40, 33, 32, 20, 27, 15, 21, 24, 23, 27, 25, 34, 17, 29, 28, 10, 25, 18, 40, 29, 27, 43, 26, 26, 31, 31, 29, 42, 31, 20, 35, 36, 31, 22, 33, 14, 21, 23, 23, 41, 20, 35, 12, 22, 27, 14, 20, 17, 30, 25, 13, 41, 37, 42. 13, 27, 36, 42, 40, 40, 21.

Среднее значение прироста оказалось равным 30,51 см. При таком ко­личестве измерений можно считать, что среднее значение мало изменит­ся, если число наблюдений будет увеличиваться. Возникает вопрос: а можно ли использовать меньшее число измерений? Оказывается, можно. Суще­ствует раздел математики, называемый математической статистикой, в котором разрабатываются способы оценки погрешностей и обосновыва­ется необходимая повторность наблюдений (число измерений).

Выпишем для примера из рассмотренного списка прирост каждой пя­той сосны. Мы получим случайную выборку из 20 деревьев:

34, 37, 30, 43. 36, 38, 36, 22, 33, 21, 34, 25, 43, 29, 36, 21, 35, 20, 41, 36.

Среднее из этих значений равно 32,5 см. Чтобы определить, насколь­ко оно может отличаться от истинного, за которое принят средний прирост из 100 измерений, в соответствии с правилами статистики найдем сначала отклонения измеренных высот прироста от их среднего значения:

1,5 4,5 -2,5 10,5 3,5 5,5 3,5 -10,5 0,5 -11,5

1,5 -7,5 10,5 -3,5 3,5 -11,5 2,5 -12,5 8,5 3,5

Вычислим сумму квадратов этих отклонений. Она равна 1009.

Полученное значение делим на число измерений, уменьшенное на еди­ницу (20-1 = 19). Результат называется дисперсией выборки (D). Она равна 1009:19 = 53,1.

Квадратный корень из дисперсии называется среднеквадратическим отклонением и обозначается греческой буквой σ(«сигма»). Это не менее важный параметр, чем среднее значение, и его всегда следует приво­дить в отчетах о наблюдениях и измерениях.

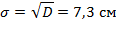
Теперь можно найти погрешность оценки среднего. Она равна отноше­нию среднеквадратического отклонения к корню квадратному из числа измерений, умноженному на коэффициент t, который зависит от количе­ства измерений и может быть найден из табл. 11.1:

Найдем погрешность средней величины прироста сосны:

Среднее значение обычно записывают вместе с величиной погреш­ности:

М = 32,5 ± 3,4 см.

Эта запись означает, что истинное среднее значение лежит в пределах от 29,1 до 35,9 см.

Следует еще раз подчеркнуть, что при расчете среднего значения ка­кой-либо величины в отчете необходимо привести четыре числа:

1) само среднее значение;

2) погрешность среднего значения;

3) среднеквадратическое отклонение;

4) количество измерений.

Если какой-либо из этих параметров отсутствует, ценность работы значительно снижается, поскольку становится трудно оценить достовер­ность полученных данных.

При многократном проведении одного и того же эксперимента резуль­таты измерений можно считать выборкой из бесконечного множества всех возможных результатов. Среднее значение измеренной величины и его погрешность вычисляются точно так же, как в предыдущем примере.