Разновидности опор балочных систем

Балка — конструктивная деталь в виде прямого бруса, закреп­ленная на опорах и изгибаемая приложенными к ней силами.

Высота сечения балки незначительна по сравнению с длиной. Жесткая заделка (защемление) (рис. 6.2)

Опора не допускает перемещений и поворотов. Заделку заменя­ют двумя составляющими силы R_Ax и R_Ay и парой с моментом M_R.

Для определения этих неизвестных удобно использовать систему уравне­ний в виде

Каждое уравнение имеет одну не­известную величину и решается без подстановок.

Для контроля правильности решений используют дополнитель­ное уравнение моментов относительно любой точки на балке, например В:

Рис. 6.2

Рис. 6.3

Шарнирно-подвижная опора (рис. 6.3)

Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реак­ция направлена перпендикулярно опорной поверхности.

Шарнирно-неподвижная опора (рис. 6.4)

Опора допускает поворот вокруг шарнира и может быть заме­нена двумя составляющими силы вдоль осей координат.

Рис. 6.4

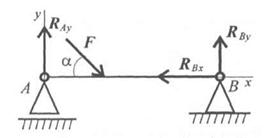
Рис. 6.5

Не известны три силы, две из них — вертикальные, следова­тельно, удобнее для определения неизвестных использовать систему уравнений во второй формуле:

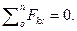
Составляются уравнения моментов относительно точек крепле­ния балки. Поскольку момент силы, проходящей через точку креп­ления, равен 0, в уравнении останется одна неизвестная сила.

Из уравнения определяется реакция R_Bx.

Из уравнения определяется реакция R_By.

Из уравнения определяется реакция R_Ay.

Для контроля правильности решения используется дополни­тельное уравнение

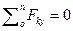
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):

Рис. 6.6

{

Контрольные вопросы и задания

1. Замените распределенную нагрузку сосредоточенной и опре­делите расстояние от точки приложения равнодействующей до опо­ры А (рис. 6.9).

Рис. 6.9

2. Рассчитайте величину суммарного момента сил системы относительно точки А (рис. 6.10).

Рис. 6.10

3. Какую из форм уравнений равновесия целесообразно использовать при определение реакций в заделке?

4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?

5. Определить реактивный момент в заделке одноопорной балки, изображенной на схеме (рис. 6.11).

Рис. 6.11

6. Определите вертикальную реакцию в заделке для балки, представленной на рис. 6.11.