КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Значение категории в формальной логике. Логические отношения между понятиями.
Слово «категория» происходит от греческого слова kategoria что значит высказывать, быть сказуемым. Категории для Аристотеля суть возможные предикаты какого-либо единичного предмета, т.е. такие понятия, которые можно высказать относительно того или иного единичного предмета или класса предметов.
Вот эти категории:
1. Субстанция (substantia).
2. Количество (quantitas).
3. Качество (qualitas).
4. Отношение (relatio).
5. Место (ubi).
6. Время (quando).
7. Положение (situs).
8. Обладание (habitus).
9. Действие (actio).
10. Страдание (passio).
Под эти десять категорий, по мнению Аристотеля, подходит всё то, что можно мыслить. Если мы желаем высказать о тех или других вещах что-либо самое общее, то мы не можем о них высказать ничего другого, кроме того, что они суть или субстанции, или что они обозначают качество, отношение, место и т.п. Других точек зрения, кроме тех, которые содержатся в категориях, не существует. Таким образом, можно сказать, что категории представляют собой наиболее общие классы всего мыслимого.
В новейшей философии в качестве наиболее общих классов мыслимого философы различают вещь, свойство, отношение. Всё, о чём мы можем мыслить, есть или вещь (субстанция), или это есть свойство (атрибут), или, наконец, это есть отношение.
Под вещами мы понимаем то, что обладает большим или меньшим постоянством формы. Например, таким постоянством обладают камень, дерево, жидкость в сосуде и т.п. Кусок камня сегодня обладает той же формой, какой он обладал вчера: нам представляется, что такое постоянство будет ему присуще и впоследствии.
Вещи мы представляем или имеющими известные свойства или качества, или совершающими известные действия, или находящимися в известном состоянии. Например, то, что кусок железа имеет известную тяжесть, есть его свойство, или качество. Если кусок железа накалён, то это есть его состояние: если кусок железа плавится или движется, то это есть известный процесс, состояние. Свойства, действия, состояния мы представляем принадлежащими известной вещи как известной носительнице их. Но в то же время мы их мыслим как элементы, из которых состоит вещь: мы мыслим железо как нечто, имеющее известную тяжесть, твёрдость, способность накаляться, приходить в движение и т.п. Качество, действие, состояние мы будем называть одним общим именем – свойства вещи.
Одна вещь может мыслиться нами находящейся в различных отношениях к другой вещи. Одна вещь может быть больше, чем другая (пространственное отношение); одна вещь может быть причиной другой вещи (причинное отношение); одна вещь может возникнуть раньше, чем другая (временное отношение), и т.п.
Всё, что мы можем мыслить, мы должны мыслить под одной из этих категорий, т.е. всё, что мы мыслим, мы должны мыслить или как вещь, или как свойство вещи, или как отношение. Эти три наиболее общих понятия мы и считаем категориями.
Этим исчерпывается вопрос о категориях.
Отношения могут существовать только между сравнимымипонятиями. Сравнимыми называются понятия, имеющие в своем содержании общие существенные признаки, то есть такие, для которых можно найти ближайшее общее родовое понятие. Например, понятия «адвокат» и «прокурор» имеют ближайшее общее родовое понятие «юрист». Несравнимыепонятия не имеют общих существенных признаков, поэтому для них нельзя подобрать ближайшее общее родовое понятие. Например, понятия «право» (род — «система социальных норм») и «дерево» (род — «растение»). Ввиду того, что отношения между несравнимыми понятиями невозможны, ниже будут рассмотрены отношения, существующие между сравнимыми понятиями.
Сравнимыепонятия в свою очередь делятся на совместимые и несовместимые Совместимыми называются понятия, объемы которых полностью или частично совпадают. Между совместимыми понятиями могут быть отношения равнозначности, подчинения и перекрещивания.
 АВА
Рис.1. АВА
Рис.1.
|
1. Равнозначность. В подобном отношении находятся понятия, объемы которых полностью совпадают, хотя их содержание может различаться Примеры равнозначных понятий «Петр I» и «1-ый российский император»; «договор банковского вклада» и «депозит». Объемы равнозначных понятий изображаются кругами Эйлера, полностью совпадающими (рис.1):
А – понятие «Кража»,
В – понятие «тайное хищение чужого имущества»
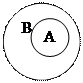
2. Подчинение. Это отношение характеризуется тем, что объем одного понятия целиком входит в объем другого понятия, но не исчерпывает его Это отношения рода и вида. Примеры - «государство» и «республика», «хищение» и «кража». Понятие с большим объемом называется подчиняющим, понятие с меньшим объемом — подчиненным.
Графическое изображение данного отношения следующее (рис.2):
Рис.2.
| А – понятие «преступление», В – понятие «уголовное преступление». |
3. Перекрещивание. Указанные отношения будут у понятий, объемы которых совпадают лишь частично Примерами подобных понятий являются следующие пары: «офицер» и «любитель пения»; «юрист» и «охотник». Данные понятия графически изображаются пересекающимися кругами Эйлера (рис.3):
| А – понятие «убийца», В – понятие «рецидивист» |
Рис.3.
Несовместимыми называются понятия, объемы которых ни полностью, ни частично не совпадают. Между несовместимыми понятиями существуют отношения соподчинения, противоречия и противоположности.
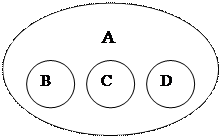
1. Соподчинение. Это отношение между несколькими понятиями, объемы которых исключают друг друга, но входят в объем общего родового понятия. Пример: понятия «лейтенант», «капитан», «майор» соподчинены понятию «офицер». Графически отношение соподчинения изображаются следующим образом (рис.4):
Рис.4.
| А – понятие «офицер», В – понятие «лейтенант», С – понятие «капитан», D – понятие «майор». |
2. Противоречие. Подобное отношение существует между двумя понятиями, которые являются видами одного и того же рода, при этом одно из понятий содержит определенные признаки, а другое эти же признаки отрицает, не утверждая никаких новых признаков. По объему два противоречащих понятия исчерпывают объем родового понятия. Отношение противоречия иначе называется отношением контрадикторности или контрадикторной противоположности. Пример, «черный» и «нечёрный»; «виновный» и «невиновный». Для графического изображения противоречащих понятий берется разделенный пополам круг Эйлера (рис.5):
Рис.5. | А – понятие «виновный», ┐А – понятие «невиновный». |
3. Контрарность, или контрарная противоположность. В этом отношении находятся два понятия, которые являются видами одного и того же рода, при этом одно из понятий содержит определенные признаки, а другое эти же признаки отрицает, заменяя их другими, исключающими. По объему два контрарных понятия, в отличие от противоречащих, контрадикторных, не исчерпывают объем родового понятия. Например, «мудрый» и «глупый»; «черный» и «белый». Графически изображается в одном круге, когда с противоположных сторон хордами рассекаются части круга (рис.6):
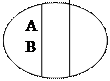 Рис.6.
Рис.6.
| А – понятие «мудрый», В – понятие «глупый». |
В качестве вывода следует отметить, что на логические отношения между понятиями большую роль оказывает степень сравнимости и несравнимости понятий. Мы не можем работать с понятиями, которые ни по объёму, ни по содержанию не имеют ничего общего. Следует чётко понимать, о чём мы думаем, т.е. улавливать объём и содержание понятия, иметь представление о мыслимом понятии, разбираться в свойствах мыслимого понятия. Отношения между понятиями представлены в обобщающей схеме (рис. 9) учебник В.И. Кириллова, А.А. Старченко. Логика. М., 2007.
Дата добавления: 2015-04-11; просмотров: 334; Мы поможем в написании вашей работы!; Нарушение авторских прав |