
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Элементы высшей математики.
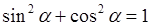 ,
, 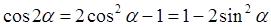 ,
,
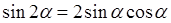 ,
, 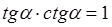 .
.
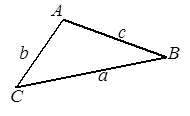 Рис. 4.
Рис. 4.
|
Теорема синусов. Отношение длин сторон к синусам лежащих против них углов в любом треугольнике одинаково (рис. 4).
 .
.
Таблица 1.
Значения синусов некоторых углов.
| a | 7,5° | 15° | 22,5° | 30° | 45° | 60° | 67,5° | 75° | 82,5° |
| sina | 0,131 | 0,259 | 0,383 | 0,5 | 0,707 | 0,866 | 0,924 | 0,966 | 0,991 |
Таблица 2.
Производные элементарных функций.
| Функция F(t) | ta | at | logat | sint | cost |
| Производная F/(t) | a ta–1 | at lna | (t lna)–1 | cost | –sint |
Производная от сложной функции.
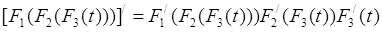 .
.
Например, 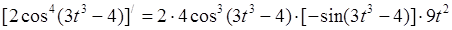 .
.
Вектор 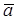 определяется значениями его трёх проекций: ax, ay, az.
определяется значениями его трёх проекций: ax, ay, az.
Модуль вектора и значения косинусов направляющих углов, задающих положение линии действия вектора, определяются выражениями:
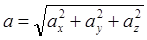 ,
, 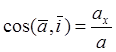 ,
, 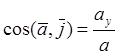 ,
, 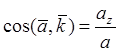 .
.
Алгебраическая сумма двух векторов равна вектору, проекции которого определяются выражениями:
 Þ
Þ 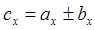 ,
, 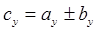 ,
, 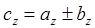 .
.
Скалярное произведение двух векторов равно числу, которое можно определить одной из формул:
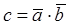 Þ
Þ 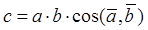 ,
, 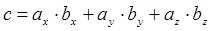 .
.
Скалярное произведение вектора самого на себя равно квадрату его модуля: 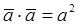 .
.
Векторное произведение двух векторов равно вектору, модуль которого определяется выражением:
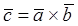 Þ
Þ 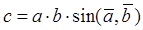 .
.
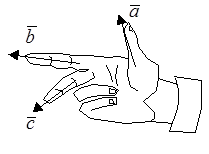 Рис. 5.
Рис. 5.
|
Векторноепроизведение вектора самого на себя равно нулю: 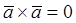 .
.
Направление вектора, равного векторному произведению двух векторов, определяет правило правой руки (рис. 5).
Направление большого пальца правой руки надо совместить с направлением первого вектора, направление указательного пальца – с направлением второго вектора, тогда средний палец, направленный перпендикулярно плоскости первых двух, покажет направление вектора, равного векторному произведению.
Дата добавления: 2015-04-15; просмотров: 344; Мы поможем в написании вашей работы!; Нарушение авторских прав |