Касательное и нормальное и полное ускорения движущейся точки.

Определим ускорение точки, когда её движение задано естественным способом. Подставив выражение (6) в формулу (2), получим:

.

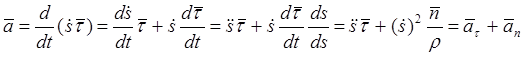Касательное ускорение точки характеризует изменение вектора её скорости по величине. Вектор касательного ускорения направлен по касательной к траектории движущейся точки в ту же сторону, что и вектор скорости точки, когда движение точки ускоренное, и в обратную сторону, когда – замедленное. Величина касательного ускорения равна первой производной по времени от величины скорости точки:

. (7)

Если касательное ускорение точки равно нулю, то точка движется равномерно.

Нормальное ускорение точки характеризует изменение вектора её скорости по направлению. Вектор нормального ускорения направлен по главной нормали к траектории движущейся точки в сторону вогнутости траектории. Величина нормального ускорения равна отношению квадрата скорости точки к радиусу кривизны её траектории:

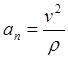. (8)

Если нормальное ускорение точки равно нулю, то точка движется прямолинейно.

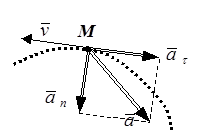Рис. 14.

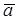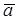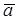Зная касательное и нормальное ускорение точки, её полное ускорение можно построить (рис. 14), как диагональ прямоугольника со сторонами, равными _t и _n.

Величина полного ускорения точки определяется по теореме Пифагора:

.

Полное ускорение точки характеризует изменение вектора скорости этой точки во времени (и по величине и по направлению).

На рис. 14 полное ускорение точки построено для случая её замедленного движения, так как направление векторов скорости и касательного ускорения противоположно.