КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематические характеристики тела при вращательном движении.
Рис. 17.
|
Осью вращениятеланазывается прямая линия, проходящая через две неподвижные точки этого тела.
Любая точка тела, лежащая на его оси вращения (рис. 17), неподвижна.
Плоскость I неподвижна. Плоскость II «вморожена» в тело и вращается вместе с ним. Обе плоскости проходят через ось вращения.
Угол j (рис. 17) между этими плоскостями полностью определяет положение вращающегося тела в пространстве. Угол j измеряется в радианах. Если известно, как изменяется угол j во времени, то говорится, что задан закон (уравнение) вращательного движения:
.
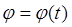Угловой скоростьютела называется кинематическая характеристика w, определяющая изменение угла j во времени. Размерность угловой скорости – радиан в секунду [1/с=с-1]. Величина угловой скорости вращающегося тела равна первой производной по времени от угла поворота тела вокруг оси вращения:
. (11)
Вектор угловой скорости вращающегося тела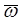 
направлен по оси его вращения по правилу правого винта (рис. 17).
Угловым ускорениемтела называется кинематическая характеристика e, определяющая изменение угловой скорости тела w во времени. Размерность углового ускорения – радиан в секунду в квадрате [1/с2=с-2]. Величина углового ускорения вращающегося тела равна первой производной по времени от величины его угловой скорости:
. (12)
Вектор углового ускорения вращающегося тела 
направлен по оси его вращения в ту же сторону, что и вектор угловой скорости (рис. 17), когда вращение ускоренное, и в обратную сторону, когда – замедленное.
Дата добавления: 2015-04-15; просмотров: 183; Мы поможем в написании вашей работы!; Нарушение авторских прав |