Вращательная скорость. Формула Эйлера.

Рис. 20.

Пусть при движении точки M расстояние от неё до некоторой прямой линии W остается неизменным. Зададим движение точки M векторным способом. Введем (рис. 20) радиус-вектор , начало которого находится в любой точки O₁ линии W, а конец совпадает с движущейся точкой M. При движении точки M изменяется только направление радиус-вектора .

Вращательная скорость точки M вокруг прямой линии W равна векторному произведению вектора угловой скорости 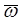вращения радиус-вектора на сам радиус-вектор :

. (19)

Вектор 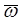угловой скорости вращения радиус-вектора направлен по прямой линии W по правилу правого винта (рис. 20).

Вектор вращательной скорости направлен (рис. 20) по правилу правой руки (рис. 5). Величина вращательной скорости определяется выражением: v=w h_W, где h_W – расстояние от точки M до линии W.

Итак, скорость любой точки вращающегося тела может быть определена, как вращательная скорость вокруг оси вращения тела (19).