Скорость точек вращающегося тела.

Рис. 18.

Траектория любой точки M вращающегося тела представляет собой окружность, лежащую в плоскости, перпендикулярной оси вращения (рис. 18). Центр этой окружности совпадает с точкой пересечения оси вращения тела с плоскостью окружности, а радиус окружности равен расстоянию MO от точки до оси вращения.

Зная траекторию, движение точки вращающегося тела можно задать естественным способом (рис. 18). Длина дуги траектории, заключенной между произвольной точкой O₁, выбранной за начало отсчета, и движущейся точкой M, (рис. 18) равна произведению плоскостного угла j (рис. 17) на расстояние MO от точки до оси вращения:

.

Теперь, используя (6), определим алгебраическую величину скорости точки вращающегося тела:

.

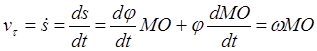Вектор скорости точки вращающегося тела направлен перпендикулярно оси вращения тела и перпендикулярно прямой, соединяющей эту точку с осью вращения тела.

Величина скороститочки вращающегося тела равна произведению угловой скорости тела на расстояние от точки до оси вращения:

. (15)