Тема 4. Способы изучения стохастических (корреляционных) взаимосвязей в экономическом анализе

Задание 4.

Для изучения связи между зависимой инезависимой величинами на базе отобранных данных:

1) постройте корреляционную таблицу, характеризующую зависимость результа­тивного признака от факторного. Сделайте выводы о характере связи между признаками;

2) изобразите связь между изучаемыми признаками графически;

3) постройте уравнение регрессии по сгруппированным данным. Параметры уравнения определите методом наименьших квадратов. Рассчитайте теоретические (полученные по уравнению регрессии) значения результативного признака. Определите форму связи между признаками;

4) на основе F-критерия Фишера и t-критерия Стьюдента проверьте значимость: в первом случае - уравнения регрессии; во втором - его параметров. Дайте экономическую интерпретацию параметров уравнения связи;

5) по сгруппированным данным вычислите линейный коэффициент корреляции и корреляционное отношение. Сделайте выводы о степени и направлении связи между изучаемыми признаками;

6) с экономической точки зрения сформулируйте выводы относительно иссле­дуемой вами связи.

Решение.

Расчетная таблица для определения параметров уравнения регрессии (парная регрессия) :

Таблица 8

N п/п	X	Прирост населения Y	X2	XY	Y2
	10,74	-11550	115,3476	-124047		-10631,2
	9,00	-17742	81,0	-159678		-8849,1
	10,69	-9865	114,2761	-105456,8		-10580,0
	10,16	-5754	103,2256	-58460,64		-10037,2
	10,10	-9389	102,01	-94828,9		-9975,7
	11,44	-12163	130,8736	-139144,72		-11348,1
	11,93	-3322	142,3249	-39631,46		-11850,0
	9,19	-9409	84,4561	-86468,71		-9043,7
	8,75	-15031	76,65	-131521,25		-8593,1
Итого:	92,00		950,1639	-939237,53		-939237,53

Используя таблицу 8, построим уравнение регрессии:

-846,4а₁=866870

а₁=-1024,2

92а₀ - 973157,9=-939237,5

92а₀=33920,4

а₀=368,7

Получим уравнение прямой вида:

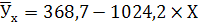
Данные для расчетов оформим в виде таблицы.

Таблица 9

№п/п
	-11550	-10631,2	-918,8	844193,44	-2127,5	4526256,25
	-17742	-8849,1	-8892,9	79083670,41	-8319,5	69214080,25
	-9865	-10580,0	715,0		-442,5	195806,25
	-5754	-10037,2	4283,2	18345802,24	3668,5	13457892,25
	-9389	-9975,7	586,7	344216,89	33,5	1122,25
	-12163	-11348,1	-814,9	664062,01	-2740,5	7510340,25
	-3322	-11850,0		727267,84	6100,50	37216100,25
	-9409	-9043,7	-365,3	133444,09	13,5	182,25
	-15031	-8593,1	-6437,9	41446556,41	-5608,5
ИТОГО:	-94225	90908,1	-3316,9	214099954,49	-9422,50

На основе t-критерия Стьюдента проверим значимость параметров уравнения регрессии.

=4877,38

Вычислим расчетные (фактические) значения t-критерия:

для параметра :

для параметра :

=1,0488

a=5,0

v=n-2=9-2=7

t_табл =2,365

Вывод: т.к. t_расч>t_табл, то параметры а₀ и а₁ признаются значимыми.

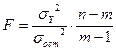
m – число параметров в уравнении регрессии.

s_у = 9156,19

s_ост = 4877,38

v₁ = m – 1=2 – 1=1

v₂ = n – m= 9 – 7=2

F_табл=5,59

Вывод: т.к. F_расч > F_табл (24,67 > 5,59) больше чем в 4 раза, то уравнение регрессии статистически значимо, т.е. доля вариации, обусловленная регрессией, намного превышает случайную ошибку и уравнение регрессии пригодно для практического использования.

Корреляционное отношение-h представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выровненных значений результативного признака d, т.е. рассчитанных по уравнению регрессии, со средним квадратическим отклонением (фактических) значений результативного признака s:

или

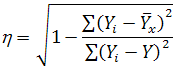
При линейной форме уравнения применяется показатель тесноты связи – линейный коэффициент корреляции

s_X=1,0488

s_Y=9156,19

Вывод: линейный коэффициент корреляции принял положительное значение, что указывает на прямую связь.

Для оценки значимости коэффициента корреляции-r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.

где (n-2) – число степеней свободы при заданном уровне значимости a и объеме выборки n.

s_y=9156,19

Вывод: линейный коэффициент корреляции принял положительное значение, что указывает на прямую связь.

=173,7

=172,5

s_X1=1,0488

s_X2=2,51

Вывод: линейный коэффициент корреляции принял отрицательное значение, что указывает на обратную связь.

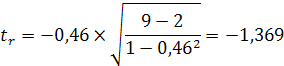
Множественный коэффициент корреляциивычисляется при наличиилинейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков:

В случае оценки тесноты связи между Y, X₁, X₂ множественный коэффициент корреляции определяется по следующей формуле:

Задание 5.

Для изучения связи между зависимой и независимой величинами на базе отобранных данных:

1) определите результативный и не менее 2-х факторных признаков. Оцените с экономической точки зрения важность факторов и последовательность их включения в уравнение регрессии;

2) определите форму корреляционного уравнения и обоснуйте его выбор. Проанализируйте характер связей;

3) постройте расчетную таблицу для определения параметров уравнения регрес­сии. Постройте множественное уравнение регрессии. Параметры уравнения регрессии определите методом наименьших квадратов;

4) рассчитайте линейные (парные) коэффициенты корреляции, проверьте их зна­чимость. Проанализируйте характер парных зависимостей между признаками. Исключите коллинеарно связанные факторы. Рассчитайте множественный коэффициент корреляции и проверьте его значимость;

5) проверьте значимость уравнения регрессии на основе:

· F-критерия Фишера;

· Средней ошибки аппроксимации;

6) проверьте значимость коэффициентов регрессии на основе t-критерия Стьюдента.