
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Статистическое наблюдение – это начальная стадия экономико-статистического исследования
Статистическое наблюдение – это начальная стадия экономико-статистического исследования. Она представляет собой научно организованную работу по сбору массовых первичных данных о явлениях и процессах общественной жизни.
По данным статистического ежегодника «Российский статистический ежегодник» Госкомстата России выбираем объект наблюдения – население Российской Федерации - статистическую совокупность, состоящую из 36 единиц наблюдения. В качестве пследних выступают регионы России, а также экономически связанные и существенные показатели: число постоянного населения на 1января, число родившихся и число умерших человек. Все показатели взяты за 2008 год (прил. Ж).
Группировка – один из основных наиболее распространенных методов обработки и анализа первичной статистической информации.
Выбор группировочных признаков всегда должен быть основан на анализе качественной природы изучаемого явления.
Группировочные признаки могут быть атрибутивными и количественными. Атрибутивные признаки регистрируются в виде текстовой задачи, например, социальная группа населения, половозрастная составляющая. Количественные признаки имеют цифровое выражение: размер дохода, стаж работы и др.
В качестве группировочных признаков нами выбрано число родившихся и умерших на 1000жителей.
Расчеты этих показателей представлены в табл. 1.
Таблица 1
Данные о числе родившихся и умерших в расчете на 1000 жителей по регионам России по состоянию на 1 января 2008г.
| № п.п | Число родившихся на 1000 жителей по регионам России | Число умерших на 1000 жителей по регионам России | |||
| Белгородская область | 11,05 | Белгородская область | 14,76 | ||
| Брянская область | 10,90 | Брянская область | 17,67 | ||
| Владимирская область | 10,74 | Владимирская область | 18,71 | ||
| Воронежская область | 9,80 | Воронежская область | 17,68 | ||
| Ивановская область | 10,31 | Ивановская область | 19,24 | ||
| Калужская область | 10,43 | Калужская область | 17,28 | ||
| Костромская область | 11,24 | Костромская область | 17,99 | ||
| Курская область | 10,69 | Курская область | 18,27 | ||
| Липецкая область | 10,76 | Липецкая область | 17,09 | ||
| Московская область | 10,53 | Московская область | 16,66 | ||
| Орловская область | 10,16 | Орловская область | 17,16 | ||
| Рязанская область | 10,04 | Рязанская область | 18,50 | ||
| Смоленская область | 10,10 | Смоленская область | 19,65 | ||
| Тамбовская область | 9,19 | Тамбовская область | 17,70 | ||
| Тверская область | 10,68 | Тверская область | 20,60 | ||
| Тульская область | 9,00 | Тульская область | 20,34 | ||
| Ярославская область | 10,37 | Ярославская область | 17,34 | ||
| г.Москва | 10,29 | г.Москва | 11,86 | ||
| Республика Карелия | 11,12 | Республика Карелия | 16,12 | ||
| Республика Коми | 12,10 | Республика Коми | 12,67 | ||
| Архангельская область | 11,93 | Архангельская область | 14,54 | ||
| Вологодская область | 11,95 | Вологодская область | 16,29 | ||
| Калининградская область | 11,29 | Калининградская область | 15,31 | ||
| Ленинградская область | 8,75 | Ленинградская область | 17,96 | ||
| Мурманская область | 10,69 | Мурманская область | 11,94 | ||
| Новгородская область | 10,56 | Новгородская область | 20,79 | ||
| Псковская область | 9,97 | Псковская область | 21,51 | ||
| г.Санкт-Петербург | 10,38 | г.Санкт-Петербург | 14,60 | ||
| Республика Адыгея | 12,69 | Республика Адыгея | 14,86 | ||
| Республика Дагестан | 18,40 | Республика Дагестан | 5,88 | ||
| Республика Ингушетия | 18,44 | Республика Ингушетия | 3,13 | ||
| Кабардино-Балкарская Республика | 13,52 | Кабардино-Балкарская Республика | 9,08 | ||
| Республика Калмыкия | 15,24 | Республика Калмыкия | 10,42 | ||
| Карачаево-Черкесская Республика | 14,88 | Карачаево-Черкесская Республика | 11,07 | ||
| Республика Северная Осетия-Алания | 14,20 | Республика Северная Осетия-Алания | 11,35 | ||
| Самарская область | 11,44 | Самарская область | 15,28 | ||
1. Определяем число групп по формуле:
n = 1+3,322´lg N,
где n - число групп;
N - число единиц совокупности;
N=36
n=1+3,322´ lg36»6,169
2. Выбираем шаг интервала таким, чтобы в одну группу не попало бы свыше половины всех единиц совокупности и в средних группах было бы больше единиц , чем в крайних. Исходя из этих уточнений, выделяем 6 групп с шагом равным 0,8:
Первая группа: до 9 человек;
Вторая группа: 9 – 9,8;
Третья группа: 9,8 – 10,6;
Четвертая группа: 10,6 – 11,4;
Пятая группа: 11,4 – 12,2;
Шестая группа: свыше 12,2.
Результаты изложим в таблице 2.
Таблица 2
| № п/п | Группы регионов по числу родившихся на 1000 жителей. | Число регионов. | Структура, %. |
| до 9 чел | 5,56 | ||
| 9 - 9,8 | 5,56 | ||
| 9,8 - 10,6 | 30,56 | ||
| 10,6 - 11,4 | 27,78 | ||
| 11,4 - 12,2 | 11,11 | ||
| свыше 12,2 | 19,43 | ||
| Итого: | 100,00 |
Для выражения статистических показателей используем относительную форму. С целью характеристики долей отдельных частей в общем объеме совокупности рассчитаем относительные величины структуры:
До 9 чел. = 2 х 100% : 36 = 5,56 %;
(9,8 – 10,6) = 11 х 100% : 36 = 30,56% и т.д. по остальным группам.
Вывод: По данным табл. 2 видно, что наибольшее количество регионов – 11 единиц, составляют регионы с числом, родившихся от 9,8-10,6 чел. на 1000 жителей. Их доля в общем количестве равна 30,56%.
Средняя величина– это обобщающий показатель, характеризующий типический уровень явления. Он определяется делением усредненной величины на сумму единиц совокупности. Средние величины делятся на два класса:
¾ степенные средние;
¾структурные средние.
В качестве структурных средних рассматриваются мода и медиана. Степенные средние подразделяются на: среднюю арифметическую, среднюю гармоническую, среднюю геометрическую, среднюю квадратическую, кубическую и т.д.
Перечисленные средние объединяются в общей формуле (при различной величине k):

где  - средняя величина исследуемого явления;
- средняя величина исследуемого явления;
Хi – i-й вариант осредняемого признака 
fi – вес i-го варианта.
Все расчетные значения занесем в аналитическую таблицу 3.
Таблица 3
Вспомогательная таблица для расчета средней величины
| №п/п | Группы регионов по числу родившихся на 1000 жителей. | Число регионов. fi | Хi | Хifi |
| до 9 чел | 8,6 | 17,2 | ||
| 9 - 9,8 | 9,4 | 18,8 | ||
| 9,8 -10,6 | 10,2 | 112,2 | ||
| 10,6 -11,4 | 11,0 | 110,0 | ||
| 11,4 -12,2 | 11,8 | 47,2 | ||
| свыше 12,2 | 12,6 | 88,2 | ||
| Итого: | 393,6 |
Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной.
Средняя арифметическая взвешенная определяется по формуле:


Итак, среднее количество родившихся на 1000 жителей в России за 2007г. составляет 10,93чел.
Для характеристики статистических рядов применяются также абсолютные показатели. Самым простым абсолютным показателем является размах вариации (R). Он показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака.
Для исследуемого ряда размах вариации составляет:
R=(12,2+0,8) - (9-0,8) =4,8
Данные для нахождения среднего линейного отклонения, среднего квадратического отклонения и дисперсии занесем в таблицу 4.
Таблица 4
| № п/п | Группы регионов по число родившихся на 1000жителей | Вес (fi) |

|

|

|

|

|

|

|
| до 9чел | 8,6 | 17,2 | -2,3 | 2,3 | 4,6 | 5,29 | 10,58 | ||
| 9-9,8 | 9,4 | 18,8 | -1,5 | 1,5 | 3,0 | 2,25 | 4,50 | ||
| 9,8-10,6 | 10,2 | 112,2 | -0,7 | 0,7 | 7,7 | 0,49 | 5,39 | ||
| 10,6-11,4 | 11,0 | 110,0 | 0,1 | 0,1 | 1,0 | 0,01 | 0,1 | ||
| 11,4-12,2 | 11,8 | 47,2 | 0,9 | 0,9 | 3,6 | 0,81 | 3,24 | ||
| свыше 12,2 | 12,6 | 88,2 | 1,7 | 1,7 | 11,9 | 2,89 | 20,23 | ||
| Итого: | 393,6 | 31,8 | 11,74 | 44,04 |
Среднее линейное отклонение(d) представляет собой среднюю величину из отклонений вариантов признака от их средней. Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариантов Хi и Х(взвешенная или простая в зависимости от исходных условий) по следующим формулам:
 (взвешенная),
(взвешенная),
простая:


Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсии (в зависимости от исходных данных):
 (взвешенная) ,
(взвешенная) ,
простая:


Среднее квадратическое отклонение – корень квадратный из дисперсии.
 ,
,

Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах, что и признак (в мерах, тоннах, рублях, процентах и т.д.)
Для целей сравнения колеблемости различных признаков в одной и той же совокупности используются показатели вариации, приведенные в относительных величинах. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего они выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности.
Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Рассчитаем следующие относительные показатели вариации:
А) коэффициент осцилляции (VR)
VR = R : Хсред. х 100% = 4,8 : 10,93 х100% = 43,92%;
Б) линейный коэффициент вариации (Vd)
Vd = dсред. х 100% : Хсред. = 0,88 х 100% : 10,93 = 8,05%;
В) коэффициент вариации (Vσ)
Vσ = σ : Хсред. х 100% = 1,104 х 100% : 10,93 = 10,1%.
Вывод: совокупность является однородной, т.к. коэффициент вариации равен 10,1%, что меньше 33%.
Мода(Мо)- значение признака, наиболее часто встречающееся в исследуемой совокупности. Расчет моды осуществляется по формуле:

где Хо – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
i – величина модального интервала;
fМо – частота модального интервала;
fМо-1 - частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Медианой (Ме) называется значение признака, приходящееся на середину ранжированной совокупности.
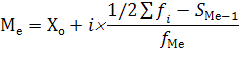
где Хо – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
i – величина медианного интервала;
SМе-1 – накопленная частота интервала, предшествующего медианному;
fМе – частота медианного интервала.
Таблица 5
Вспомогательная таблица для определения моды, медианы, квартилей.
| № п/п | Группы регионов по число родившихся на 1000жителей | Вес | Накопленная частота. |
| до 9 чел | |||
| 9 - 9,8 | |||
| 9,8 - 10,6 | |||
| 10,6 - 11,4 | |||
| 11,4 - 12,2 | |||
| Свыше 12,2 | |||
| Итого |

 =10,84
=10,84
Для характеристики размера вариации признака используется квартильное отклонение. Оно определяется по формуле:
dк = (Q3 – Q1) : 2, где Q3 и Q1 – соответственно третья и первая квартили распределения.
Квартили представляют собой значение признака, делящие ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний Q1, отсекающий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний Q3, отсекающий ¾ части совокупности с наибольшими значениями признака.

где ХQ1 – нижняя граница интервала, содержащего нижний квартиль;
i – величина интервала;
fQ1 – частота интервала, содержащего нижний квартиль;
SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль. То же самое и для верхнего квартиля.


Дата добавления: 2015-04-15; просмотров: 222; Мы поможем в написании вашей работы!; Нарушение авторских прав |