Тема 2. Понятие о закономерностях распределения

Задание 2. Проверьте гипотезу о нормальном законе распределения статистических данных, полученных в результате наблюдения .

Решение. На основе вышеприведенных и обработанных статистических данных проверим гипотезу о нормальном законе распределения с помощью критерия Пирсона .

Таблица 6

Расчет теоретических частот нормального распределения

Группы регионов по числу родившихся на 1000 жителей.	( )
до 9 чел		8,6	-2,110	0,0431	1,1243	0,876	0,683
9 - 9,8		9,4	-1,385	0,0153795	0,4017	1,598	6,309
9,8 - 10,6		10,2	-0,661	0,032068	0,8374	10,163	123,342
10,6 - 11,4		11,0	0,063	0,39814	10,3852	-0,385	0,014
11,4 - 12,2		11,8	0,788	0,29246	7,6304	-3,630	1,727
свыше 12,2		12,6	1,512	0,12722	3,3183	3,682	4,086
ИТОГО:							0,9084

Критерий Пирсона определяется по следующей формуле:

.

Нормальное распределение выражается следующей стандартизированной кривой нормального распределения:

где - ордината кривой нормального распределения;

- стандартизованное отклонение;

е и p -математические постоянные;

Х - варианты вариационного ряда;

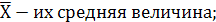
s - среднее квадратическое отклонение.

t=2,110

2,11=0,0431

2,12=0,0422

0,0431-0,0422=0,0009

0,0009´0=0

у_t=0,0431-0=0,0431

f_t1= (0,8*36/1,104)*0,0431=1,1243

f_t2= (0,8*36/1,104)*0,0154=0,4017

f_t3= (0,8*36/1,104)*0,0321=0,8374

f_t4= (0,8*36/1,104)*0,3981=10,3852

f_t5= (0,8*36/1,104)*0,2925=7,6304

f_t6= (0,8*36/1,104)*0,1272=3,3183

f_э-f_t1 =2-1,1243=0,876

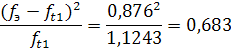
c²=0,9084 Р=0,50

у=n-3=6-3=3 (число степеней свободы в нормальном распределении равно числу групп минус 3). По специальной таблице определяем табличное значение: c²=14,8 (при числе степеней свободы 3).

Вывод: т.к. c²_{расчетный} меньше c²_{табличного} (0,9084<14,8), можно говорить, что гипотеза о близости эмпирического распределения к нормальному подтверждается.