Цементной печи

В [1] изложено решение задачи идентификации на основе решения уравнения Винера-Хопфа с применением среды Delphi7.0, в которой было разработано программное приложение. При этом для вычисления оценок корреляционных функций составляется алгоритм, реализующий следующие соотношения

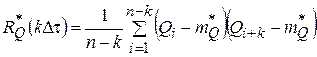, (2)

, (3)

где Q_i=Q[i], q_i=q[i] – значения случайного сигнала в i-ом сечении; m_Q^* и m_q^* – оценки мат. ожиданий; R_Q^* и R_Qq^* – оценки корреляционной и взаимокорреляционной функций случайных процессов.

Программная среда Delphi 7.0 является хорошим средством написания объектно-ориентированных программ и программ, связанных с различными базами данных, но не обладает необходимыми для наших целей библиотеками математических функций, и для целей математического моделирования гораздо удобнее использовать специализированные математические пакеты, такие как MathCAD или MATLAB.

С целью унификации программного средства для получения математической частной модели процесса обжига клинкера была разработана программа в среде MATLAB, которая позволяет получать корреляционные функции, взаимные корреляционные функции исследуемых сигналов, весовые функции, переходные функции. Для оценки точности вычислений с использованием предложенного инструментария было произведено сравнение найденных графиков с расчетами, полученными в среде MathCAD. Проверка показала хорошее совпадение получаемых расчетных данных и графиков.

Стоит отметить, что определение корреляционных функций в MATLAB производится гораздо проще, чем в среде программирования Delphi7.0, поскольку в перовй для этого существует специальная математическая функция xcorr, которую можно использовать в расчетах.

Функция вычисления взаимной корреляции векторов и матриц хсоrr имеет несколько форм записи [2], которые представлены ниже:

С=хсоrr (А,В) - для векторов А и В с длиной М > 1 возвращает оценку взаимной корреляции в виде вектора С длиной 2М – 1 (в ином случае возвращает 0);

xcorr(A) при векторе А возвращает оценку автокорреляции;

хсоrr (.. ,SCALE0PT) - задает способ масштабирования корреляционной функции. Значение SCALE0PT определеяет следующие вычисления:

'biased' - вычисляется смещенная оценка корреляционной функции как 1/М;

'unbiased' - вычисляется несмещенная оценка корреляционной функции как 1/(M-abs(lags));

'coeff' - осуществляется масштабирование так, чтобы значение корреляционной функции при нулевом смещении было равно 1,0;

'none' - масштабирование не производится (задано по умолчанию).

Применение функции хсоrr иллюстрирует следующий пример:

ryu=xcorr(y2,u2,'biased');

ryu3=ryu(n:n+tm-2);

где y2, u2 - векторы, содержащие значения выходного и входного сигнала соответственно, n - размер векторов.

После применения функции хсоrr второй строкой выделяется область положительных значений, поскольку функция возвращает вектор значений корреляционной функции от –n до n. На рис.2. показаны графики вычисленных с использованием данной функции корреляционной функции входа и взаимной корреляционной функции между входом и выходом.

Как видно корреляционные функции удовлетворяют требованиям эргодических стационарных процессов и стремятся с течением времени к нулю.

Решая интегральное уравнение Винера-Хопфа (1) численными методами, его сводят к решению системы алгебраических уравнений с числом уравнений равным количеству полученных ординат корреляционных функций (2) - (3). При этом интеграл в уравнении (1) представляется конечной суммой:

. (4)

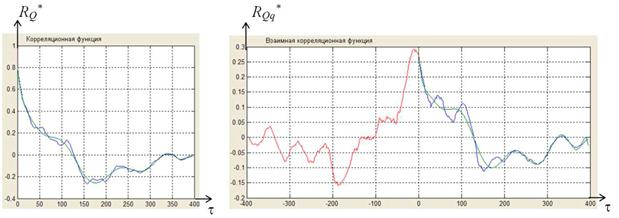
А б

Рис. 2. Оценки: а - корреляционной функции входа, б - взаимной