
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
АНАЛИЗ НЕРАЗВЕТВЛЕННОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Цель работы: изучить особенности неразветвленной электрической цепи при различных соотношениях индуктивного и емкостного сопротивлений.
1. Общие сведения.
Схема замещения неразветвленной электрической цепи, содержащей индуктивную катушку и конденсатор представлена на рис.14.
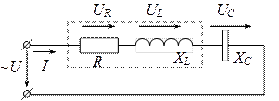 Рис. 14. Электрическая цепь с последовательным соединением R, L, C
Рис. 14. Электрическая цепь с последовательным соединением R, L, C
|
Проанализируем данную электрическую цепь – рассмотрим значения тока цепи I, напряжения на отдельных участках UR, UL, UC, полной, активной, реактивной мощностей.
Так как при последовательном соединении элементов R, L, C ток является общим для всех элементов цепи, то удобно принять
i = Im sinωt.
По II Закону Кирхгофа
u = uR + uL + uC.
или
u = UmахRsinωt + UmахLsin(ωt + π/2) + UmахC sinωt(ωt - π/2) =
= UmахRsinωt + (UmахL - UmахC)sin(ωt + π - π/2) =
= UmахRsinωt + (UmaxL - UmaxC)sinωt(ωt + π/2).
Таким образом, полное напряжение цепи состоит из двух синусоидальных слагаемых одинаковой частоты, а, следовательно, являются так же синусоидальными с некоторой амплитудой Umах и фазовым углом φ (при условии, что начальная фаза тока равна 0).
u = Umах sin(ωt + φ).
 Рис. 15. Векторные диаграммы при различных соотношениях XL и XC :
а) XL > XC б) XL, < XC с) XL = XC
Рис. 15. Векторные диаграммы при различных соотношениях XL и XC :
а) XL > XC б) XL, < XC с) XL = XC
|
Векторные диаграммы тока и напряжений цепи при различных соотношениях XL и XC показаны на рис.
Из векторных диаграмм следует, что вектора напряжений образуют треугольник напряжений, в котором гипотенуза – входное напряжение цепи U, катет, прилегающий к углу φ - активная составляющая напряжения UR, второй катет UL – UC = UP – реактивная составляющая напряжения
UR = Ucosφ; UP = Usinφ;

Если в треугольнике напряжений все стороны разделить на ток I, то получим треугольник сопротивлений (рис. 16а), а если умножить на I2 – треугольник мощностей (рис. 16б).
 Рис. 16. а) треугольник сопротивлений; б) треугольник мощностей.
Рис. 16. а) треугольник сопротивлений; б) треугольник мощностей.
|
Из треугольника сопротивлений:
R = Z cosφ; X = Z sinφ; 
Из треугольника мощностей
P = S cosφ; Q = S sinφ; S = 
Из треугольников определяют
cosφ = UR/U = R/Z = P/S.
Свое название cosφ получил из треугольника мощностей – коэффициент мощности – важный показатель электрооборудования. Определяет, какую часть от полной мощности составляет активная мощность, мощность, расходуемая на совершение полезной работы.
Комплексные ток и напряжения:
İ = I e j0.
 =
=  ejφ =
ejφ =  +
+  +
+  = I(R + I jXL - I jXC )= I(R + j(XL -XC)).
= I(R + I jXL - I jXC )= I(R + j(XL -XC)).
Разделив обе части уравнения на İ, получим комплексное сопротивление цепи:
Z = U ejφ/ Iej0 =Z ejφ = R + j(XL – XC),
где  – модуль комплексного сопротивления, или полное сопротивление цепи; R – активное сопротивление цепи; XL – XC = Х -реактивное сопротивление цепи; φ – аргумент комплексного сопротивления, равный углу сдвига фаз между векторами напряжения и тока φ = arctg(XL – XC)/R.
– модуль комплексного сопротивления, или полное сопротивление цепи; R – активное сопротивление цепи; XL – XC = Х -реактивное сопротивление цепи; φ – аргумент комплексного сопротивления, равный углу сдвига фаз между векторами напряжения и тока φ = arctg(XL – XC)/R.
При последовательном соединении элементов с R, L, C ток в цепи

В зависимости от соотношений между индуктивным и емкостным сопротивлениями в электрической цепи с последовательным соединением индуктивной катушки и конденсатора имеют место три характерных режима:
– режим недокомпенсации реактивного сопротивления, когда ток отстает от напряжения (XL>XC), 90°>φ>0;
– режим, перекомпенсации реактивного сопротивления, когда ток опережает
напряжение (XC > XL), 0 < φ < – 90°;
– режим компенсации реактивного сопротивления, когда ток и напряжение совпадают по фазе (XC = XL), φ = 0°.
Из всех возможных соотношений между индуктивным XL и емкостным XС сопротивлений особый интерес представляет случай, когда эти сопротивления равны, т. е. ХL = ХС. В этом случае реактивное сопротивление X = XL – XC = 0 и полное сопротивление цепи Z = R минимально. Тогда ток в цепи I = U/R и при U = const, R = const значение его максимально.
Напряжения на индуктивном и емкостном элементах по значению
UL = XLI = XCI = UC.
Следовательно,
UL = XL I = XL U/R; UC = XC I = XC U/R.
Таким образом, напряжения на индуктивном и емкостном элементах могут превышать напряжение сети в XL/R раз, если XL>R.
 Рис. 17. Векторная диаграмма для режима резонанса напряжений.
Рис. 17. Векторная диаграмма для режима резонанса напряжений.
|
Cдвиг по фазе между напряжениями UL и UC равен π, т.е. эти напряжения находятся в противофазе.
Такой режим цепи при последовательном соединении элементов с R, L и C, когда XL = XC , а напряжения на индуктивном (UL) и емкостном (UC) элементах, находящихся в название режима резонанса напряжений.
Векторная диаграмма напряжений для резонанса напряжений представлена на рис. 17. Реактивная составляющая напряжения равна нулю; следовательно, полное напряжение U = Uа, а угол сдвига фаз
φ = 0; cosφ = 1.
Активная мощность такой цепи P = U I cosφ = U I = S, а реактивная
Q = U I sinφ = 0. В режиме резонанса напряжений реактивные мощности индуктивной катушки (QL = XL I2) и конденсатора (QC =XC I2) равны между собой, но обратны по знаку. Происходит непрерывный обмен энергией между магнитным полем катушки и электрическим полем конденсатора.
Равенства индуктивного и емкостного сопротивлений ωL = 1/(ωC) можно добиться, изменяя угловую частоту ω, индуктивность L или емкость С. Угловая частота, при которой наступает резонанс напряжений,
ω0 = 1/  .
.
 Рис. 18. Зависимость напряжений и тока от частоты.
Рис. 18. Зависимость напряжений и тока от частоты.
|
При этой резонансной частоте, ток в цепи достигает максимального значения. При уменьшении частоты увеличивается сопротивление XC = 1/ (ωC), а следовательно, и реактивное сопротивление цепи X = XL – XC cтановится не равным нулю. Ток I = =U/  уменьшается. При частоте ω = 0, что формально соответствует напряжению постоянного тока, ток в цепи равен нулю (XС = бесконечности) реактивное сопротивление цепи тоже становится больше нуля и ток начинает уменьшаться (рис. 18).
уменьшается. При частоте ω = 0, что формально соответствует напряжению постоянного тока, ток в цепи равен нулю (XС = бесконечности) реактивное сопротивление цепи тоже становится больше нуля и ток начинает уменьшаться (рис. 18).
Падение напряжения на элементе с активным сопротивлением
UR = R I изменяется так же, как ток в цепи, т. к. R = const. При этом UR = U при ω = ω0.
Зафиксировать наступление резонанса напряжений можно:
– По показанию амперметра (он покажет максимальное значение силы тока);
– По показанию вольтметра (напряжения на катушке и конденсаторе будут приблизительно равны);
– По показанию ваттметра (ваттметр покажет максимальное значение активной мощности).
Явление резонанса напряжений используют в устройствах радиотехники, телевидения, автоматики и других электроустройствах.
Если электрическая цепь имеет такие L и С, что резонансной для этой цепи является частота ω0 =  , то ток этой частоты будет максимальным. Токи других частот (если в цепи действуют несколько напряжений разной частоты) будут меньше. Изменяя индуктивность L или емкость С можно настроить контур на эту частоту, т. е. усилить ток этой цепи.
, то ток этой частоты будет максимальным. Токи других частот (если в цепи действуют несколько напряжений разной частоты) будут меньше. Изменяя индуктивность L или емкость С можно настроить контур на эту частоту, т. е. усилить ток этой цепи.
В электросиловых устройствах это явление не нашло применения, так как в режиме резонанса напряжений резко увеличиваются напряжения UL и UC, что может привести к пробою их изоляции.
2. Домашнее задание по подготовке к лабораторному занятию:
– изучить материал, указанный в литературе;
– письменно ответить на контрольные вопросы, представленные в 4 пункте лабораторной работы;
– при заданных напряжении сети U, параметрах катушки Rk, Lk, частоте сети f = 50 Гц согласно номеру варианта (табл. 3) рассчитать емкость конденсатора С для получения резонанса напряжения в исследуемой цепи, рассчитать ток Iрез. в этом режиме, а также напряжения на индуктивной катушке UL-R и конденсаторе UС;
Таблица 3
| Номер варианта | ||||||||
| U, В | 33,8 | 34,0 | 33,9 | 33,9 | 33,9 | 33,9 | ||
| Lк,мГн | ||||||||
| Rk, Ом | 55,4 | 45,9 | 76,5 | 84,7 | 38,1 | 47,5 | 38,2 | 38,0 |
– полученные данные занести в табл. 4.;
Таблица 4
| C, мкФ | Iрез, А | UL-R, В | UC, В | Примечание |
– подготовить бланк отчета к лабораторному занятию.
Дата добавления: 2015-04-16; просмотров: 298; Мы поможем в написании вашей работы!; Нарушение авторских прав |