ЛАБОРАТОРНАЯ РАБОТА № 4

ИССЛЕДОВАНИЕ ЦЕПИ ТРЕХФАЗН0Г0ТОКА ПРИСОЕДИНЕНИИ ПРИЕМНИКОВ ПО СХЕМЕ «ЗВЕЗДА»

Цель работы: изучить влияние величины и характера нагрузки в одной из фаз приемника на фазное и линейное напряжения, напряжение смещения нейтрали в 3-проводной цепи и на ток в нейтральном проводе в 4-проводной цепи.

1. Обще сведения

Система трехфазного переменного электрического тока была предложена в конце 19 века. Благодаря работам Н. Теслы, Г. Феррариса и М.О. Доливо-Добровольского трехфазный ток быстро завоевал общее признани. Генераторы трехфазного тока, двигатели, использующие его энергию, – это наиболее совершенные, экономичные и надежные электрические машины, превосходящие по большинству технико-экономических показателей, как машины постоянного тока, так и машины однофазного переменного тока. Неоспоримы преимущества 3-фазного тока при передаче энергии на расстояние (исключая сверхмощные линии электропередачи протяженностью в несколько тысяч километров). В цепях 3-фазного тока путем несложных переключений можно подучить различные напряжения и мощности. Поэтому массовая электрификация промышленности началась, по существу, с появления 3-фазного тока.

Вообще m-фазной цепью называют совокупность электрических цепей, в которых действуют созданные общим источником синусоидальные ЭДС одинаковой частоты и амплитуды, сдвинутые между собой по фазе на 2π/m. Для 3-фазиой цепи m=3, и сдвиг по фазе между ЭДС, приложенными к отдельным цепям, составляет 120° (2π/3).

Отдельные цепи, входящие в состав 3-фазной цепи, принято наливать фазами и маркировать буквами «А», «В», «С». Тогда, если принять (т.е. начальная фаза Ψ_А=0), то 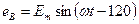, а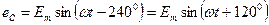

В комплексном выражении ; ; .

Безразлично какая из фаз будет принята за первую; важно только, что ЭДС следующей по порядку фазы от нее отстает, а ЭДС третьей фазы – опережает, При этом соблюдается порядок чередования фаз А–B–C (или В–С–А, или С–А–В).

Очевидно, и .

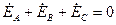Приемники соединяются по схеме «звезда» в том случае, когда их номинальное напряжение равно фазному напряжению источника. Соединение по схеме «звезда» – это такая схема, при которой три конца фазных приемников (или фазных обмоток источника) соединяются в общую точку («нейтраль»), а три начала выводятся в линию. Естественно, понятия «начало» и «конец» являются условными и применяются только для определения направления ЭДС (или противоЭДС) в катушках. При отсутствии ЭДС (противоЭДС) маркировка начал и концов не имеет смысла.

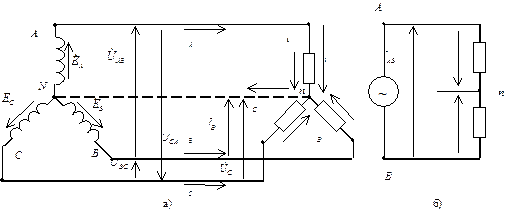Рис. 27. Соединение по схеме «звезда» источника и приемника

На рис. 27 показано соединение по схеме «звезда» как источника, так и приемника энергии.

Ток, протекающий по фазе электроприемника, называется фазным, а ток в линейном проводе между источником и приемником – линейным. На рис. 27 видно, что при соединении по схеме «звезда» цепь фазного тока – это продолжение цепи линейного тока, т.е. линейный ток равен фазному.

Напряжение между началом и концом фазы называется фазным, а между выводами разноименных фаз - линейным. Так, па рис. 27а фазные 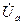напряжения: , , линейные (междуфазные) напряжения: , , . Вобщем случае , , , что непосредственно вытекает из рис. 27б.

При анализе 3-фазной цепи исходят из того, что источник всегда является симметричным ( ), а приемник может быть как симметричным, ( ), так и не симметричным. Очевидно, что при симметричном приемнике токи в фазах равны 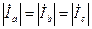. В этом случае потенциалы нейтралей источника и приемника: .

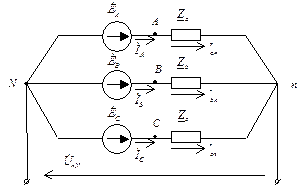Рис. 28. Соединение по схеме «звезда»

При соединении по схеме «звезда» несимметрия фазных нагрузок приводят к перераспределению потенциалов в цепи, между точками N и n появляется разность потенциалов, называемая смещением нейтрали (Рис.28).

Как видно из рис. 12 , т.е.

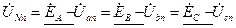
где , , .

В соответствий с методом узловых напряжений между узлами N и n

где , , – комплексные проводимости фазных цепей.

При симметричной нагрузке проводимости равны, и т.к

, .

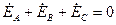В этом случае

, ,

(внутренним сопротивлением фаз источника и сопротивлением линейных проводов пренебрегаем): фазные напряжения на зажимах приемника образуют симметричную систему, они равны по величине и сдвинуты по фазе ровно на 120°. Поэтому

и ;

Рис. 29. Векторная диаграмма цепи приемника с симметричной нагрузкой

Векторная диаграмма такой цепи показана на рис. 29:

; .

Как и в однофазной цепи, угол φ определяется соотношением активного и реактивного сопротивлений в каждой фазе. Так, 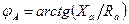и т.д.

Векторы линейных напряжений (U_AB, U_BC, U_CA,) построены как геометрические разности соответствующих фазных. Нетрудно видеть, что по модулю они больше фазных в 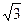раз,

.

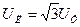При несимметричной нагрузке , и хотя 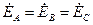, фазные напряжения , , не равны между собой, существенно различаясь в зависимости от , что представляет серьезные неудобства для потребителей энергии, электрическое состояние такой цепи принято иллюстрировать топографической (потенциальной) векторной диаграммой, на плоскости которой координаты каждой точки соответствуют величине потенциалов изображаемых точек электрической цепи (рис. 30). В принятом масштабе расстояние между точками топографической диаграммы равно разности потенциалов (напряжению) между изображаемыми точками электрической цепи (например, цепи на рис. 27а).

Рис. 30. Векторная диаграмма цепи приемника с несимметричной нагрузкой

Точка N, изображающая нейтраль источника энергии, находится на рис. 30 в центре симметрии равностороннего треугольника линейных напряжений. Точка n, эквипотенциальная N в случае симметричной нагрузки, здесь смещается в соответствии с величиной и направлением вектора . Векторы, соединяющие точку n с вершинами А, В, С, - фазные напряжения 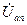, , . Здесь же построена векторная диаграмма токов в предположении активного характера нагрузки по фазам ( 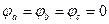), По-прежнему

, но

.

Преобразуя выражение, можно показать что

.

Существуют электроустановки с заведомо несимметричной нагрузкой (жилые дома, столовые, лаборатории, электросварочные участки и т.п.). Для того, чтобы обеспечить симметрию фазных напряжений в таких установках, нужно уравнять потенциалы нейтралей N и n, чтобы . Это достигается прокладкой нейтрального (четвертого) провода в 3-фазной цепи между точками N и n (cм. рис. 27а).

Возникает переток зарядов по нейтральному проводу - ток , причем, как видно из рис. 27а, по первому закону Кирхгофа:

.

Нельзя забывать о том, что данное уравнение (как, впрочем, и все остальные) справедливо только в комплексном выражении.

При наличии нейтрального провода , фазные напряжения становятся равны между собой, векторная диаграмма напряжений повторяет рис. 29, а на векторной диаграмме токов появляется ток .

Мощность 3-фазной цепи складывается из мощностей отдельных фаз:

.

В случае симметричной нагрузки

Если, как обычно, воспользоваться не фазными, а линейными значениями токов и напряжений, то при симметричной нагрузке

.

Аналогичные выражения определяют реактивную и полную мощность 3-фазной цепи. Средневзвешенный коэффициент мощности

.