Расчет эмпирических коэффициентов линейной функции

Год
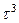
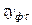
Сумма

Решая систему уравнений для определения параметров линейной функции:

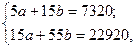имеем:

Результат прогноза на 2006 год:

Результаты предварительных расчетов среднего квадратического отклонения сведём в таблицу 9.

Среднее квадратическое отклонение от линейного тренда:

.

Ширина доверительного интервала (при ):

.

Интервальный прогноз: или

.

Таблица 9

Предварительные расчеты среднего квадратического отклонения от линейного тренда

№	Год	Количество проданных автомобилей, шт.,	Вид уравнения

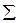
Для параболы система уравнений, решая которую необходимо определить коэффициенты 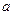, и , имеет вид:

.

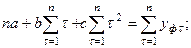
После подстановки расчётных значений:

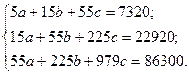
Решая данную систему уравнений, получаем:

, , .

Результат прогноза на 2006 год:

Результаты предварительных расчетов среднего квадратического отклонения сведём в таблицу 10.

Таблица 10

Предварительные расчеты среднего квадратического отклонения от параболического тренда

№	Год	Количество проданных автомобилей, шт.,	Вид уравнения
			1274,9
			1366,6	275,6
			1461,2	353,4
			1558,6
			1658,9	1,2
				730,2

Среднее квадратическое отклонение от параболического тренда:

.

Ширина доверительного интервала (при ): .

Интервальный прогноз: или .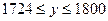

Таким образом, при аппроксимации предложенного динамического ряда линейной функцией прогноз на 2006 год будет иметь следующий вид: , а при аппроксимации параболической функцией: .

Аппроксимация более универсальный метод прогнозирования, чем экстраполяция по темпу роста или прироста. Если в полученные аналитические функции подставить значения 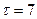; 8 и т.д., то можно получить прогнозные объемы реализации соответственно на 2007 и 2008 гг. В том случае, когда задача заключается в определении временного периода после которого годовой объем реализации превысит, например, 2000 автомобилей, то из выражения:

,

находим порядковый номер временного периода:

который соответствует 2009 году.

Недостатком аппроксимации можно считать равноценность членов динамического ряда. Практика показала, что влияние динамики более поздних периодов сказывается на развитие исследуемого процесса более существенно, чем более ранних. Поэтому было бы логично учитывать влияние динамики поздних периодов с большим весом, чем ранних.