Основы теории множеств.

Теория вероятностей - математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий является понятие случайного события (в дальнейшем просто событие). Отказ – событие случайное.

Событием называется всякий факт (исход), который в результате опыта (испытания, эксперимента) может произойти или не произойти. Каждому из таких событий можно поставить в соответствие определенное число, называемое его вероятностью и являющееся мерой возможного совершения этого события.

Современное построение теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств.

Множество – это любая совокупность объектов произвольной природы, каждый из которых называется элементом множества. Множества обозначаются по-разному: или одной большой буквой или перечислением его элементов, данным в фигурных скобках, или указанием (в тех же фигурных скобках) правила, по которому элемент относится к множеству. Например, конечное множество М натуральных чисел от 1 до 100 может быть записано в виде

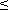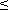М = {1, 2, …,100} = {i - целое; 1 i 100}.

Предположим, что производится некоторый опыт (эксперимент, испытание), результат которого заранее неизвестен, случаен. Тогда множество 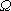всех возможных исходов опыта представляет пространство элементарных событий, а каждый его элемент (один отдельный исход опыта) является элементарным событием. Любой набор элементарных событий (любое их сочетание) считается подмножеством (частью) множества 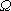и является случайным событием, т. е. любое событие А – это подмножество множеств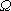а : А .

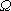В общем случае, если множество 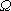содержит n элементов, то в нем можно выделить 2ⁿ подмножеств (событий).

Рассматривая событие 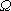(ведь каждое множество есть свое собственное подмножество), можно отметить, что оно является достоверным событием, т. е. осуществляется при любом опыте. Пустое множество как событие является невозможным, т. е. при любом опыте заведомо не может произойти.

Совместные (несовместные) события – такие события, появление одного из которых не исключает (исключает) возможности появления другого.

Зависимые (независимые) события – такие события, появление одного из которых влияет (не влияет) на появление другого события.

Противоположное событие относительно некоторого выбранного события А – событие, состоящее в не появлении этого выбранного события (обозначается ).

Полная группа событий – такая совокупность событий, при которой в результате опыта должно произойти хотя бы одно из событий этой совокупности. Очевидно, что события А и составляют полную группу событий.

Одна из причин применения теории множеств в теории вероятностей заключается в том, что для множеств определены важные преобразования, которые имеют простое геометрическое представление и облегчающее понимание смысла этих преобразований. Оно носит название диаграммы Эйлера-Венна, и на ней пространство 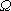изображается в виде прямоугольника, а различные множества – в виде плоских фигур, ограниченных замкнутыми линиями. Пример диаграммы, иллюстрирующей включение множеств C B А, приведен на рис. 3.1.

Рис. 3.1

Видно, что B является подмножеством А, а C – подмножеством B (и одновременно подмножеством А).