
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аксиомы теории вероятностей
Сопоставим каждому событию А число, называемое, как и прежде, его вероятностью и обозначаемое P(A) или P{A}. Вероятность выбирают так, чтобы она удовлетворяла следующим условиям или аксиомам:
P( 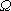 ) = 1; P( ) = 1; P(  ) = 0. ) = 0.
| (3.6) |
P(  ) ) 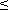 P(A) P(A) 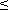 P( P( 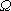 ). ).
| (3.7) |
Если Ai и Aj несовместные события, т. е. Ai 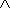 Aj =
Aj =  , то
, то
P(Ai 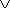 Aj) = P(Ai) + P(Aj). Aj) = P(Ai) + P(Aj).
| (3.8) |
Приведенные аксиомы постулируются, и попытка доказать их лишена смысла. Единственным критерием справедливости является степень, с которой теория, построенная на их основе, отражает реальный мир.
Аксиому (3.8) можно обобщить на любое конечное число несовместных событий { Аi }n i=1:
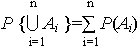
| (3.9) |
С помощью аксиом можно вычислить вероятности любых событий (подмножеств пространства 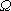 ) с помощью вероятностей элементарных событий. Вопрос о том, как определить вероятности элементарных событий, является риторическим. На практике они определяются либо из соображений, связанных с возможными исходами опыта (например, в случае бросания монеты естественно считать вероятности выпадения орла или решки одинаковыми), или на основе опытных данных (частот).
) с помощью вероятностей элементарных событий. Вопрос о том, как определить вероятности элементарных событий, является риторическим. На практике они определяются либо из соображений, связанных с возможными исходами опыта (например, в случае бросания монеты естественно считать вероятности выпадения орла или решки одинаковыми), или на основе опытных данных (частот).
Последний подход широко распространен в прикладных инженерных задачах, поскольку позволяет косвенно соотнести результаты анализа с физической реальностью.
Предположим, что в опыте пространство 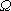 можно представить в виде полной группы несовместных и равновозможных событий А1, А2, …, Аn. Согласно (3.3) их сумма представляет достоверное событие:
можно представить в виде полной группы несовместных и равновозможных событий А1, А2, …, Аn. Согласно (3.3) их сумма представляет достоверное событие:
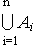 =
= 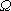 .,
.,
так как события А1, А2, …, Аn несовместны, то согласно аксиомам (3.6) и (3.9):
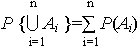 = P( = P( 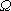 ) = 1. ) = 1.
| (3.10) |
Поскольку события А1, А2, …, Аn равновозможны, то вероятность каждого из них одинакова и равна

Отсюда непосредственно получается частотное определение вероятности любого события A:
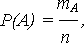
| (3.11) |
как отношение числа случаев (mA), благоприятных появлению события А, к общему числу случаев (возможному числу исходов опыта) n.
Совершенно очевидно, что частотная оценка вероятности есть не что иное как следствие аксиомы сложения вероятностей. Представив, что число n неограниченно возрастает, можно наблюдать явление, называемое статистическим упорядочением, когда частота события А все меньше изменяется и приближается к какому-то постоянному значению, которое и представляет вероятность события А.
Дата добавления: 2015-04-16; просмотров: 283; Мы поможем в написании вашей работы!; Нарушение авторских прав |