
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные законы и правила теории вероятностей
Вероятности сложных событий можно вычислять с помощью вероятностей более простых, пользуясь основными правилами (теоремами): сложения и умножения вероятностей.
II.2.4.1. Теорема сложения вероятностей.
Если А1, А2, …, Аn - несовместные события и А – сумма этих событий, то вероятность события А равна сумме вероятностей событий А1, А2, …, Аn:

| (3.12) |
Эта теорема непосредственно следует из аксиомы сложения вероятностей (3.8).
В частности, поскольку два противоположных события А и  несовместны и образуют полную группу, то сумма их вероятностей
несовместны и образуют полную группу, то сумма их вероятностей
P(A) + P(  ) = 1 ) = 1
| (3.13) |
Чтобы сформулировать в общем случае теорему умножения вероятностей, введем понятие условной вероятности.
Условная вероятностьсобытия А1 при наступлении события А2 – вероятность события А1, вычисленная в предположении, что событие А2 произошло:
P(А1  А2) = P(А1 А2) = P(А1  А2)/P(А2). А2)/P(А2).
| (3.14) |
II.2.4.2. Теорема умножения вероятностей.
Вероятность произведения (совместного появления) двух событий А1 и А2 равна вероятности одного из них, умноженной на условную вероятность другого, в предположении, что первое событие произошло:

| (3.15) |
Для любого конечного числа событий теорема умножения имеет вид

| (3.16) |
В случае, если события А1 и А2 независимы, то соответствующие условные вероятности

поэтому теорема умножения вероятностей принимает вид

| (3.17) |
а для конечного числа n независимых событий

| (3.18) |
Следствием правил сложения и умножения вероятностей является теорема о повторении опытов (схема Бернулли): опыты считаются независимыми, если вероятность того или иного исхода каждого из них не зависит от того, какие исходы имели другие опыты.
Пусть в некотором опыте вероятность события А равна P(А) = p, а вероятность того, что оно не произойдет P(  ) = q, причем, согласно (3.13)
) = q, причем, согласно (3.13)
P(A) + P(  ) = p + q = 1
) = p + q = 1
Если проводится n независимых опытов, в каждом из которых событие А появляется с вероятностью p, то вероятность того, что в данной серии опытов событие А появляется ровно m раз, определяется по выражению

| (3.19) |
где  - биномиальный коэффициент.
- биномиальный коэффициент.
Например, вероятность однократной ошибки при чтении 32-разрядного слова в формате ЭВМ, представляющего комбинацию 0 и 1, при вероятности ошибки чтения двоичного числа p = 10-3, составляет по (3.19)

где q = 1- p = 0,999; n = 32; m = 1.
Вероятность отсутствия ошибки чтения при m = 0, C032 = 1

Часто возникают задачи определения вероятностей того, что некоторое событие А произойдет по меньшей мере m раз или не более m раз. Подобные вероятности определяются сложением вероятностей всех исходов, которые составляют рассматриваемое событие.
Расчетные выражения для такого типа ситуаций имеют вид:

где Pn(i) определяется по (3.19).
При больших m вычисление биномиальных коэффициентов Cnm и возведение в большие степени p и q связано со значительными трудностями, поэтому целесообразно применять упрощенные способы расчетов. Приближение, называемое теоремой Муавра-Лапласа, используется, если npq>>1, а |m-np|<(npq)0,5, в таком случае выражение (3.19) записывается:

| (3.20) |
2. 5. Формула полной вероятности и формула Байеса (формула вероятностей гипотез)
В практике решения большого числа задач формула полной вероятности (ФПВ) и формула Байеса, являющиеся следствием основных теорем, находят широкое применение.
II.2.5.1.Формула полной вероятности.
Если по результатам опыта можно сделать n исключающих друг друга предположений (гипотез) H1, H2, … Hn, представляющих полную группу несовместных событий (для которой 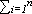 ), то вероятность события А, которое может появиться только с одной из этих гипотез, определяется:
), то вероятность события А, которое может появиться только с одной из этих гипотез, определяется:
P(A) = P(Hi )  P(A P(A  Hi ), Hi ),
| (3.21) |
где P(Hi) – вероятность гипотезы Hi;
P(А| Hi) – условная вероятность события А при гипотезе Hi.
Поскольку событие А может появиться с одной из гипотез H1, H2, … Hn, то А = АH1 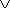 H2
H2 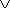 …
… 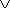 АHn , но H1, H2, … Hn несовместны, поэтому
АHn , но H1, H2, … Hn несовместны, поэтому

В виду зависимости события А от появления события (гипотезы) Hi
P(AHi) = P(Hi)· P(А| Hi), откуда и следует выражение (3.21).
2.5.2.Формула Байеса (формула вероятностей гипотез).
Если до опыта вероятности гипотез H1, H2, … Hn были равны P(H1), P(H2), …, P(Hn), а в результате опыта произошло событие А, то новые (условные) вероятности гипотез вычисляются:

| (3.22) |
Доопытные (первоначальные) вероятности гипотез P(H1), P(H2), …, P(Hn) называются априорными, а послеопытные - P(H1| А), … P(Hn| А) – апостериорными.
Формула Байеса позволяет «пересмотреть» возможности гипотез с учетом полученного результата опыта.
Доказательство формулы Байеса следует из предшествующего материала. Поскольку P(Hi  А) = P(Hi)
А) = P(Hi)  P(А| Hi) = P(Hi)
P(А| Hi) = P(Hi)  P(Hi| А):
P(Hi| А):
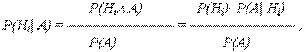
откуда, с учетом (3.21), получается выражение (3.22).
Если после опыта, давшего событие А, проводится еще один опыт, в результате которого может произойти или нет событие А1, то условная вероятность этого последнего события вычисляется по (3.21), в которую входят не прежние вероятности гипотез P(Hi), а новые - P(Hi| А):

| (3.23) |
Выражение (3.23) называют формулой для вероятностей будущих событий.
3.1. Случайные величины и их характеристики.
Случайной величиной Х называется величина, которая в результате опыта может принять то или иное значение, причем заранее неизвестное. Различают дискретные и непрерывные случайные величины.
Дискретная случайная величина – величина, принимающая только отделенные (разрозненные) друг от друга значения, которые можно заранее перечислить (например, число агрегатов, вышедших одновременно из работы).
Если дискретная случайная величина Х принимает значения Х1, Х2, …, Хm c заданными вероятностями Р1, Р2, …, Рm , то соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения.
Для дискретных случайных величин закон распределения вероятностей наиболее просто задать с помощью таблиц распределения.
Непрерывная случайная величина – величина, возможные значения которой непрерывно заполняют некоторый промежуток (интервал) – например, изменения нагрузки.
Дата добавления: 2015-04-16; просмотров: 239; Мы поможем в написании вашей работы!; Нарушение авторских прав |