
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторные диаграммы. В электрической цепи (рис
В электрической цепи (рис. 30, а) элементы R, L и С соединены последовательно и подключены к источнику синусоидального напряжения. Ток в такой цепи будет изменяться также по синусоидальному закону.
Уравнение электрического состояния цепи для мгновенных значений напряжений имеет вид и=иR+uL+uC.Если выразить иR, uL и uC через ток и параметры элементов R,L и С, получим

Уравнение электрического состояния может быть записано так же, как сумма векторов напряжений, т. е. вектор напряжения на входе цепи будет равен сумме векторов напряжений на элементах R,L и C (рис. 30, а):  .
.
►Сравнивая правые части уравнений электрического состояния, записанные для мгновенных значений и в виде векторов, можно видеть, что напряжение uR на элементе R совпадает по фазе с током, напряжение uL. на элементе L опережает ток на угол π/2 и напряжение иC на элементе С отстает от тока на угол π/2. Поэтому уравнение в виде суммы векторов можно представить как геометрическую сумму векторов на векторной диаграмме. Построение векторной диаграммы можно начать с вектора тока  , так как при последовательном соединении R,L и C он является общим для всех элементов цепи. Направим вектор тока по горизонтальной оси (рис. 30,б), векторы напряжений на участках строим при условии обхода контура против направления тока. Стрелки векторов напряжений направляются в сторону возрастающего потенциала.
, так как при последовательном соединении R,L и C он является общим для всех элементов цепи. Направим вектор тока по горизонтальной оси (рис. 30,б), векторы напряжений на участках строим при условии обхода контура против направления тока. Стрелки векторов напряжений направляются в сторону возрастающего потенциала.

Потенциал точки о приравняем к нулю (V0=0), вектор  совпадает с вектором тока и направлен от точки о к точке с. Напряжение на элементе L опережает ток на угол π/2, поэтому вектор
совпадает с вектором тока и направлен от точки о к точке с. Напряжение на элементе L опережает ток на угол π/2, поэтому вектор  строим из точки с к точке b под углом π/2 к вектору тока. Напряжение на элементе С отстает от тока на угол π/2, следовательно, вектор
строим из точки с к точке b под углом π/2 к вектору тока. Напряжение на элементе С отстает от тока на угол π/2, следовательно, вектор  необходимо направить в сторону отставания, т. е. на диаграмме из точки b вниз до точки с (UC<UL). Соединив конец вектора
необходимо направить в сторону отставания, т. е. на диаграмме из точки b вниз до точки с (UC<UL). Соединив конец вектора  с началом координат, получим вектор напряжения источника
с началом координат, получим вектор напряжения источника  .
.
Векторы  ,
,  и
и 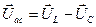 образуют прямоугольный треугольник напряжений, из которого получим
образуют прямоугольный треугольник напряжений, из которого получим
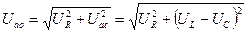
Поделив напряжение на ток, получим выражения для полного сопротивления:

где X= ХL - ХC - реактивное сопротивление электрической цепи.
На векторной диаграмме этому выражению соответствует треугольник сопротивлений опгп. Индуктивное и емкостное сопротивления характеризуют свойства цепи, обусловленные ее реакцией на изменение тока и напряжения, поэтому их называют реактивными.
Из треугольника сопротивлений можно определить угол сдвига фаз φ между током и напряжением по формулам:  , или
, или  . Зная
. Зная 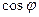 или
или  , по тригонометрическим таблицам определяют угол φ.
, по тригонометрическим таблицам определяют угол φ.
ЗАПОМИНИТЕ
В электротехнике условились угол φ обозначать стрелкой, направленной от вектора тока к вектору напряжения. Знак угла φ в выражении для мгновенного значения тока i определяется характером нагрузки: при индуктивном характере нагрузки (XL>ХC) ток отстает от напряжения на угол φ и в выражении для мгновенного значения тока угол φ записывают со знаком минус, т. е.  ; при емкостном характере нагрузки (ХC>ХL) ток опережает напряжение и угол φ в выражении мгновенного значения тока записывают со знаком плюс, т. е.
; при емкостном характере нагрузки (ХC>ХL) ток опережает напряжение и угол φ в выражении мгновенного значения тока записывают со знаком плюс, т. е. 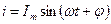 .
.
ПРИМЕР В схеме электрической цепи (рис. 30, а) напряжения на элементах равны: UR= 40 В; UL=30 В; UC=60 В. Определить напряжение на входе цепи Uao (напряжение источника) и напряжения на участках Uac и Ubo. Векторная диаграмма построена на рис. 30, б.
Рассмотрим электрическую цепь, состоящую из двух приемников, подключенных параллельно к зажимам источника синусоидального напряжения  (рис. 31, а). В первом приемнике включены последовательно элементы R1 и L, во втором соответственно R2 и С. Оба приемника находятся под действием одного общего напряжения.
(рис. 31, а). В первом приемнике включены последовательно элементы R1 и L, во втором соответственно R2 и С. Оба приемника находятся под действием одного общего напряжения.
Выражение для мгновенных значений токов в первой и второй ветвях заданной цепи имеют соответственно индуктивный и емкостный характер.
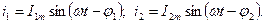
Действующее значение тока I и косинус угла φ определяем из следующих выражений:
для первой ветви
 ;
; 
для второй ветви
 ;
; 
Зная токи в ветвях, нельзя определить значение тока I в неразветвленной части цепи простым сложением токов I1 и I2, так как при этом необходимо учитывать их фазовые углы φ1 и φ2. Поэтому ток I определяют как геометрическую сумму токов в ветвях, т. е.  . На рис. 31,б изображена векторная диаграмма, где произведено такое суммирование (принято I1>I2 и φ2> φ1).
. На рис. 31,б изображена векторная диаграмма, где произведено такое суммирование (принято I1>I2 и φ2> φ1).
Значения токов в ветвях и в неразветвленной части цепи можно определить и аналитически. Для этого вводят понятия активной и реактивной составляющих тока для ветви при последовательном соединении активных и реактивных элементов. Так, для первой ветви с элементами R и L

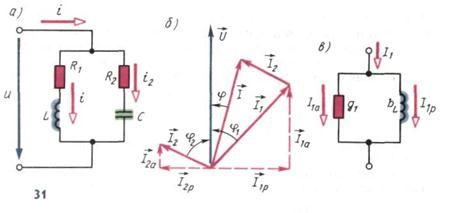
В этом случае ветвь с током I1 (его активной и реактивной составляющими) будет соответствовать двум параллельным ветвям (рис. 31, в) с проводимостями g1 и bL. В одной ветви схемы замещения будет активная составляющая тока 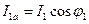 , по фазе совпадающая с напряжением; в другой - реактивная составляющая тока
, по фазе совпадающая с напряжением; в другой - реактивная составляющая тока  которая по фазе отстает от напряжения на угол ! π/2.
которая по фазе отстает от напряжения на угол ! π/2.
► Ветвь с активной составляющей тока характеризуется активной проводимостью g1, выражение для которой можно получить исходя из формулы для активной составляющей тока I1a, т. е.

где 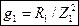 - активная проводимость первой ветви.
- активная проводимость первой ветви.
ЗАПОМНИТЕ
Активная проводимость g= R1/Z2 выражается в сименсах: 1/[Ом] =[См].
Активная проводимость ветви g1 не является величиной, обратной активному сопротивлению R1, так как в выражение полного сопротивления ветви  входит реактивная составляющая ωL.
входит реактивная составляющая ωL.
►Ветвь с реактивной составляющей тока характеризуется реактивной проводимостью bL. Выражение реактивной проводимости можно получить из формулы для I1р, т. е.

где  - реактивная проводимость первой ветви, См.
- реактивная проводимость первой ветви, См.
ЗАПОМНИТЕ
Реактивная проводимость bL не является величиной, обратной реактивному сопротивлению, так как при ее определении учитывается и активное сопротивление ветви. Полная проводимость первой ветви:

Ток в первой ветви (см. рис. 31, а) определяется по формуле I1=Y1U.
Активная составляющая тока I2а совпадает по фазе с напряжением U. Значение I2а определим по формуле

Реактивная составляющая тока I2р определяется по формуле

Активная составляющая тока Iа в неразветвленной части цепи равна сумме I1a и I2a (обе составляющие совпадают по фазе с напряжением):
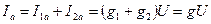
Реактивная составляющая тока первой ветви I1р отстает по фазе от напряжения на угол π/2, а реактивная составляющая тока второй ветви I2р опережает напряжение на π/2.
► Таким образом, реактивная составляющая тока Iр в неразветвленной части цепи равна разности реактивных составляющих токов I1р и I2р. Реактивная проводимость для ветви с индуктивностью bL записывается со знаком плюс, а для ветви с емкостью bC - со знаком минус.

Выражение полного тока в неразветвленной части цепи имеет вид

► При смешанном соединении ветвей расчет токов в ветвях производится методом эквивалентных преобразований с использованием проводимостей. Эквивалентное сопротивление приемника определяется через проводимости ветвей и полную проводимость разветвления.
Дата добавления: 2015-04-16; просмотров: 346; Мы поможем в написании вашей работы!; Нарушение авторских прав |