
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анализ электрических цепей с переменными элементами с помощью круговых диаграмм
► При анализе режимов в электрических цепях часто представляется необходимым определять зависимость изменения
одной какой-либо электрической величины от изменения
одного или нескольких параметров цепи. Такой анализ режима цепи можно проводить графически построением круговых диаграмм.
Круговая диаграмма — это геометрическое место концов векторов тока или напряжения при изменении по модулю какого-либо параметра исследуемой цепи при условии сохранения неизменными всех других параметров, а также частоты и входного напряжения.
Рассмотрим круговые диаграммы токов на примере простейших электрических цепей. На рис. 38, а, б представлены цепи при последовательном соединении элементов R, L и R, С. Выясним с помощью круговой диаграммы (рис. 38, в) характер изменения тока  при изменении сопротивления элементов XL и Хс-
при изменении сопротивления элементов XL и Хс-
При заданном значении напряжения питания U векторы напряжения  на
на  комплексной плоскости при изменении сопротивления R или X всегда располагаются под углом π/2. Поэтому конец вектора напряжения
комплексной плоскости при изменении сопротивления R или X всегда располагаются под углом π/2. Поэтому конец вектора напряжения  (или потенциал точки b) при изменении любого из указанных параметров будет описывать окружность, образуя так называемый годограф напряжения. Диаметр окружности равен длине вектора
(или потенциал точки b) при изменении любого из указанных параметров будет описывать окружность, образуя так называемый годограф напряжения. Диаметр окружности равен длине вектора  . При этом, если X = XL (индуктивность), то годограф образует правую полуокружность, а если X = Хс- левую.
. При этом, если X = XL (индуктивность), то годограф образует правую полуокружность, а если X = Хс- левую.
Вектор тока  совпадает по направлению с вектором
совпадает по направлению с вектором  . Поэтому при R=const и переменном X конец вектора тока
. Поэтому при R=const и переменном X конец вектора тока  будет также описывать соответствующие полуокружности. Здесь диаметр окружности равен току короткого замыкания Iк. Ток Iк подсчитывается при X = 0. Он будет активным:
будет также описывать соответствующие полуокружности. Здесь диаметр окружности равен току короткого замыкания Iк. Ток Iк подсчитывается при X = 0. Он будет активным:  .
.
Проследим за изменением вектора тока  при изменении сопротивления R и неизменном значении сопротивления реактивного элемента, например индуктивности (рис. 39, а).
при изменении сопротивления R и неизменном значении сопротивления реактивного элемента, например индуктивности (рис. 39, а).
При R = 0, что соответствует режиму короткого замыкания 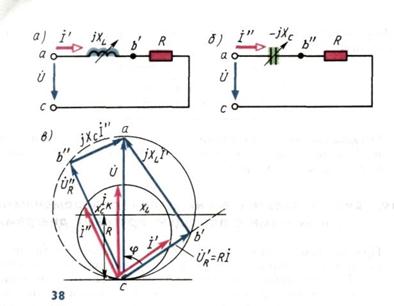
участка bс, в цепи остается только реактивный элемент L с сопротивлением XL, поэтому ток Iк будет индуктивным и его значение определится по формуле  .
.
Вектор тока 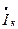 по фазе будет отставать от напряжения
по фазе будет отставать от напряжения  на угол π/2 и по направлению совпадать с осью -j (рис. 39, б). В выбранном масштабе отложим вектор тока
на угол π/2 и по направлению совпадать с осью -j (рис. 39, б). В выбранном масштабе отложим вектор тока 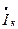 и на нем, как на диаметре, построим полуокружность. Далее для каждого задаваемого значения R будем находить комплекс тока
и на нем, как на диаметре, построим полуокружность. Далее для каждого задаваемого значения R будем находить комплекс тока  . Для этого в масштабе сопротивления по оси -j отложим катет XL (отрезок
. Для этого в масштабе сопротивления по оси -j отложим катет XL (отрезок  ). Из точки М параллельно вектору
). Из точки М параллельно вектору  проведем линию переменного параметра R. Чтобы определить ток, нужно
проведем линию переменного параметра R. Чтобы определить ток, нужно

Дата добавления: 2015-04-16; просмотров: 681; Мы поможем в написании вашей работы!; Нарушение авторских прав |