Генератора

Фазы обмотки трехфазного генератора могут быть соединены в звезду Y (рис. 50, а) или в треугольник Δ (рис. 50, б).

ЗАПОМНИТЕ

При соединении в звезду концы фаз объединяются в одну точку N (рис. 50,а), которая называется нулевой, или нейтральной. Нагрузку можно подключить к зажимам: N—А; N—В; N—С или А—В; В—С; С—А.

► Различают фазные Е_A, Е_B и Е_C и линейные Е_АВ, Е_BC и Е_СA эдс, которые связаны между собой выражениями:

В симметричной системе система линейных эдс симметрична: Ė_AB + Ė_BC + Ė_CA=0. При этом соотношение между фазными и линейными эдс имеют вид:

ЗАПОМНИТЕ

При соединении фаз источника в треугольник нагрузку подключают к его вершинам (рис. 50, б). При этом линейные и фазные эдс и напряжения оказываются равными: E_ф = Е_л; U_ф = U_л. Такое соединение возможно лишь при симметричном источнике. В этом случае фазы образуют замкнутый контур, ток в котором отсутствует.

Практически невозможно выполнить все обмотки одинаковыми, т. е. система эдс всегда несимметрична. В ней появляется уравнительный ток, что нежелательно. Поэтому обмотки генератора (за редким исключением) соединяют звездой.

ЗАПОМНИТЕ

Приемники электрической энергии могут быть соединены в треугольник и в звезду. Обычно задается значение линейного напряжения источника. Стандартом предусмотрена шкала линейных напряжений: 127, 220, 380, 500, 660 В и т. д., каждое из которых в 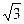раза больше предыдущего.

Пример

Задано =380 В. Записать фазные и линейные напряжения в комплексной форме.

В соответствии с векторной диаграммой рис. 50, в имеем:

= U_ф=220 В, =U_Ae^-j2π/3=(—110—j190)В, =220е^-j4π/3= (—110+j190) В, = - =(330+j190) В, = - =(-j380 В; = - =(-330 + j190)В.

§ 26. Соединение фаз нагрузки в звезду

и треугольник

Соединение фаз нагрузки в звезду

Если объединить концы фаз генератора и концы фаз нагрузки в общую точку, то получим трехфазную четырехпроводную систему (рис. 51, а).

Провода, соединяющие генератор с нагрузкой, называются линейными. Провод, соединяющий нейтральные точки источника и нагрузки, называется нейтральным.

В отдельных случаях, когда сопротивление проводов Z_л и внутреннее сопротивление источника малы и ими можно пренебречь

В каждом линейном проводе проходит свой линейный ток.

Например, в проводе А ток İ_А (он же и ток фазы источника).

► Нагрузка в трехфазной цепи может быть:

неоднородной и неравномерной, если сопротивления фаз нагрузки различны по характеру (аргументу) и значению (модулю); Z_a≠Z_b≠Z_c; φ_a≠φ_b≠φ_c; равномерной, если сопротивления фаз равны по модулю, но отличаются по характеру: Z_a=Z_b=Z_c; φ_a≠φ_b≠φ_c; однородной, если сопротивления фаз нагрузки одинаковые по характеру (аргументу), но отличаются по значению (модулю) : Z_a≠Z_b≠Z_c; φ_a=φ_b=φ_c;

симметричной, если сопротивления фаз одинаковы по значению и модулю: Z_a=Z_b=Z_c.

При симметричной нагрузке напряжение , называемое напряжением смещения потенциала нейтрали нагрузки V_n относительно нейтрали генератора V_N, равно нулю ( =0, İ_N=0), так как Ė_А+Ė_B+Ė_C=0. При несимметричной нагрузке и малом сопротивлении нейтрального провода (Z_N=0) разность потенциалов между нейтральными точками генератора и нагрузки близка к нулю( ~0) и токи в фазах определяются фазными напряжениями , и . При этом ток в нейтральном проводе İ_N=İ_А+İ_B+İ_C.

В общем случае, когда Z_a≠Z_b≠Z_c, Z_N≠0, токи фаз определяют по методу узлового напряжения. При этом полагают, что полные сопротивления, ветвей фаз А, В и С соответственно равны: Z_A=Z_a+Z_л; Z_B=Z_b+Z_л; Z_С=Z_с+Z_л; Формула для определения имеет вид

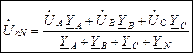
где Y_A,Y_B, Y_C, Y_N — проводимости соответственно фаз А, В, С и нейтрали.

Трехфазная трехпроводная система представлена на рис. 51, б. В этом случае сопротивление Z_N=∞, Y_N=0. Напряжение смещения нейтрали нагрузки определяют по формуле

Векторная диаграмма для общего случая ( =0) представлена на рис. 51, в. Токи в линейных проводах

При этом имеет место равенство İ_А+İ_B+İ_C=0.

Рассмотрим аварийные ситуации в трехпроводной системе.

При обрыве одной из фаз нагрузки, например фазы а, образуется однофазная цепь (Z_A =∞), в которой сопротивления фаз b и с нагрузки включены последовательно, а токи в линейных проводах В и С .

Напряжения фаз нагрузки становятся равными: ; .

Эту же электрическую цепь можно считать трехфазной и вести расчет, пользуясь формулой смещения нейтрали, принимая Y_A=0:

.

Если Y_B=Y_C, то ;

При коротком замыкании фазы нагрузки, например фазы a, Z_A =0, Y_B =∞. Напряжение смещения нейтрали

.

Следовательно, потенциал нейтрали нагрузки V_n переместился в точку а, а фазы нагрузки b и с находятся под соответствующими линейными напряжениями (рис. 51, в).