Электрические цепи с нелинейной индуктивностью. Дроссели. Магнитные усилители

В качестве нелинейной индуктивности используют катушку индуктивности с ферромагнитным сердечником (рис. 56, а). Если цепь питается от источника синусоидального напряжения и=U_msinωt, и если считать активное сопротивление и индуктивность рассеяния катушки незначительными, то все приложенное напряжение уравновешивается эдс самоиндукции e_L, наводимой переменным потоком Ф в сердечнике: , где w — число витков обмотки.

ЗАПОМНИТЕ

При синусоидальном напряжении магнитный поток Ф и эдс e_L также синусоидальны, но магнитный поток отстает по фазе от напряжения на π/2, а эдс самоиндукции в катушке e_L отстает на π/2 от потока Ф:

,

где Е_т =ωwФ_т. Действующее значение эдс в катушке

Векторная диаграмма индуктивной катушки с ферромагнитным сердечником представлена на рис. 56, б.

Ферромагнитный сердечник обычно выполняют из магнитомягкого материала, магнитная характеристика которого — динамическая петля магнитного гистерезиса (рис. 56, в, кривая 2) — отличается от статической (кривая 1) вследствие проявления инерционного действия вихревых токов. На рис. 57, а приведено

построение графика зависимости и (t). Как видно из построения при и= U_msinωt, кривая тока i(t) несинусоидальна и не совпадает по фазе с напряжением (при i = 0; и≠0).

Реальную кривую тока можно заменить эквивалентной синусоидой i_э,(t) (рис. 57, б). Угол δ называют углом потерь на перемагничивание сердечника. Такая замена позволяет использовать известные методы анализа и расчета синусоидальных электрических цепей.

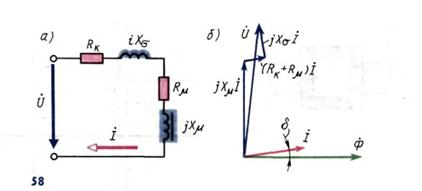
Электрическая схема цепи катушки и векторная диаграмма с учетом потока рассеяния (Ф_σ>0), потерь в обмотке (R_K > 0) и потерь на перемагничивание сердечника (R_μ>0) представлены на рис. 58, а, б соответственно. Уравнение электрического состояния цепи имеет вид .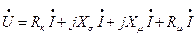

Катушку индуктивности с ферромагнитным сердечником, имеющим воздушный зазор., называют дросселем. Дроссель используется на практике как индуктивное сопротивление в электрических цепях и фильтрах.

Согласно закону полного тока для магнитной цепи дросселя, имеем wI = Н_Bl_B+ Н_стl_ст, где H_B, H_cт— напряженность магнитного поля соответственно в воздушном зазоре и сердечнике; l_B, l_ст— длина воздушного зазора и сердечника.

Подставляя значения Н_в= В_в/μ₀ =Ф/(μ₀S) и Н_ст= B_ст/(μ_rμ₀) и полагая, что R_K, X_σ и R_μ=0, получим

Индуктивность дросселя определяется по формуле

Так как , то в определенном диапазоне изменения l_B можно считать, что L =μ₀w²l_B/S. С изменением l_в изменяется L и ток в цепи I, т. е. посредством регулирования воздушного зазора в дросселе можно регулировать ток в электрической цепи переменного тока.

► Индуктивное сопротивление, создаваемое катушкой с замкнутым ферромагнитным сердечником, можно изменять подмагничиванием сердечника с помощью дополнительной обмотки, подключаемой к регулируемому источнику постоянного напряжения (рис. 59, а). Такое устройство называют дросселем с подмагничиванием.

Если пренебречь потоками рассеяния и потерями в сердечнике, то для цепи переменного тока дросселя с подмагничиванием уравнение электрического состояния для мгновенных значений имеет вид

откуда

где е_др — эдс самоиндукции, создаваемая изменением магнитного потока в сердечнике на ΔФ; R = R_к+R_н — суммарное сопротивление катушки и нагрузки; w — число витков обмотки переменного тока.

При одновременном действии переменного и постоянного токов результирующая магнитодвижущая сила F = F ₌+F_~ и соответственно поток в сердечнике Ф=Ф₌+Ф_~.

Из построения кривой тока на рис. 59,6 видно, что при Ф₌=0 ток i=i' мал. При Ф₌ > 0 ток i = i" значительно увеличивается.

ЗАПОМНИТЕ

Изменяя подмагничивающий постоянный ток, можно регулировать в широком диапазоне ток I_~. Это свойство используется в магнитных усилителях.