
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Переходные процессы в линейных электрических цепях
Для изучения данного раздела студенты должны:
1) знать законы изменения токов и напряжений в простейших электрических цепях при переходном процессе; решение уравнений электрического состояния цепи при переходном процессе;
2) понимать причины возникновения переходных процессов в электрических цепях; законы коммутации; характер изменения токов и напряжений в электрических цепях при переходных процессах; смысл и значение постоянной времени;
3) уметь составлять уравнения электрического состояния линейных электрических цепей при переходных процессах; определять постоянную времени простейших электрических цепей; определять закон изменения токов и напряжений в простейших линейных электрических цепях при переходных процессах.
Переходный (неустановившийся) процесс возникает в электрической цепи как в результате изменения параметров цепи, так и при негармоническом изменении величины приложенного напряжения.
Изучая переходные процессы, мы определяем закономерности изменения тока и напряжения в элементах электрических цепей в функции времени при переходе от одного установившегося состояния к другому. Переход от одного установившегося состояния к другому сопровождается изменением энергии магнитного поля в индуктивности  и энергии электрического поля в емкости
и энергии электрического поля в емкости 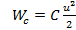 . Эти энергии не могут изменяться скачком, так как мощность, равная производной энергии по времени
. Эти энергии не могут изменяться скачком, так как мощность, равная производной энергии по времени  , должна в этом случае достигнуть бесконечно большого значения, что практически невозможно. Следовательно, если не могут скачком изменяться энергии
, должна в этом случае достигнуть бесконечно большого значения, что практически невозможно. Следовательно, если не могут скачком изменяться энергии  , то не могут изменяться скачком ток i в индуктивности L и напряжение u на емкости C, что и обусловливает законы коммутации.
, то не могут изменяться скачком ток i в индуктивности L и напряжение u на емкости C, что и обусловливает законы коммутации.
Для последовательной цепи, содержащей r, L и C , уравнение, составленное по второму закону Кирхгофа, для мгновенных значений имеет следующий вид:

| (9) |
Это уравнение справедливо для любого момента времени, следовательно, оно справедливо как для установившегося состояния, так и для переходного процесса. Уравнение (9) является неоднородным и его решение можно представить как сумму частного решения данного уравнения и общего решения однородного уравнения, которое получается из основного уравнения путем замены напряжения и нулем.
Решением уравнения для переходного процесса являются показательные и тригонометрические функции, играющие главенствующую роль при исследовании переходных процессов. Представим себе, что уравнение (9) рассматривается для установившегося состояния. Назовем ток установившегося состояния «установившимся» током и будем обозначать через i ус , тогда уравнение (9) примет вид:

| (10) |
Вычитая уравнение (10) из уравнения (9), получаем:

| (11) |
В полученном уравнении разность токов  является ничем иным, как некоторым током, который существует в электрической цепи только во время переходного процесса; напряжение u равно нулю и ток
является ничем иным, как некоторым током, который существует в электрической цепи только во время переходного процесса; напряжение u равно нулю и ток  существует как бы независимо от приложенного к цепи внешнего напряжения. В силу сказанного этот ток называют «свободным» и обозначают через
существует как бы независимо от приложенного к цепи внешнего напряжения. В силу сказанного этот ток называют «свободным» и обозначают через 

Откуда

| (11а) |
Как показывает выражение (11а), ток переходного процесса может быть получен как сумма двух токов, одним из которых является ток установившегося состояния  , определяемый как частное решение дифференциального уравнения (9), а второй - ток, который определяется как общее решение соответствующего однородного уравнения.
, определяемый как частное решение дифференциального уравнения (9), а второй - ток, который определяется как общее решение соответствующего однородного уравнения.
Заменяя  в уравнении (11) на
в уравнении (11) на  , получаем однородное дифференциальное уравнение для определения свободного тока:
, получаем однородное дифференциальное уравнение для определения свободного тока:

| (11б) |
Таким образом, для исследования переходного процесса в последовательной цепи составляется дифференциальное уравнение, описывающее переходный процесс (9), уравнение, определяющее собой ток установившегося состояния (10), и однородное дифференциальное уравнение для свободного тока (11б).
Для решения однородного дифференциального уравнения свободного тока составляется характеристическое уравнение, для чего однородное дифференциальное уравнение свободного тока записывается в алгебраической форме путем замены производной  через оператор р , а интеграл
через оператор р , а интеграл  через 1/р.
через 1/р.
Произведя указанные операции над уравнением (11б), получаем

Вынося за скобку  , получаем
, получаем
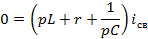
Так как  здесь не равен нулю, то
здесь не равен нулю, то

Откуда получаем искомое характеристическое уравнение

Показатель степени р определяет порядок дифференциального уравнения свободного тока. Как видно в последовательной цепи, содержащей r, L и C мы имеем дифференциальное уравнение второго порядка.
Определяем корни характеристического уравнения:
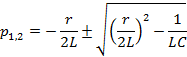
В зависимости от значения корней характеристического уравнения (соотношения между параметрами цепи r, L и C) будут получены частные решения однородного дифференциального уравнения свободного тока:
1) Если  , то решение для свободного тока имеет вид
, то решение для свободного тока имеет вид

2) Если 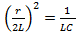 , решение для свободного тока имеет вид
, решение для свободного тока имеет вид

3) Если  , решение для свободного тока имеет вид
, решение для свободного тока имеет вид


где  – постоянные интегрирования;
– постоянные интегрирования;  - корни характеристического уравнения.
- корни характеристического уравнения.
Корни характеристического уравнения в последнем случае соответственно равны: 

Рассмотрим несколько задач.
Задача 1. Определить ток переходного процесса при подключении катушки (последовательная цепь r и L) как на постоянное, так и на синусоидальное напряжения.
Дано:  , для постоянного напряжения U=100 Вт, для синусоидального напряжения
, для постоянного напряжения U=100 Вт, для синусоидального напряжения  f=50 Гц.
f=50 Гц.
1) Постоянное напряжение. Определяем ток установившегося положения:

Уравнение свободного тока

Его характеристическое уравнение

откуда корень характеристического уравнения

Свободный ток
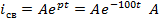
Ток переходного процесса

Определяем постоянную интегрирования A. Полагая  и учитывая, что ток в индуктивности скачком возникнуть не может (цепь до начала переходного процесса была разомкнута
и учитывая, что ток в индуктивности скачком возникнуть не может (цепь до начала переходного процесса была разомкнута  ), получим
), получим

откуда 
Таким образом, ток переходного процесса будет равен

2) Синусоидальное напряжение. Определяем установившийся ток:



Так как свободный ток не зависит от напряжения, то воспользуемся его выражением, полученным в предыдущей задаче. Тогда ток переходного процесса

Определяем постоянную интегрирования A:

откуда А=2.
Таким образом, ток переходного процесса будет равен

Задача 2. Определить ток переходного процесса в последовательной цепи с активным сопротивлением и емкостью при подключении ее как к постоянному, так и к синусоидальному напряжениям.
Дано:  , для постоянного напряжения U=100 Вт, для синусоидального напряжения
, для постоянного напряжения U=100 Вт, для синусоидального напряжения  f=50 Гц.
f=50 Гц.
1. Постоянное напряжение. Установившийся ток в цепи с емкостью, подключенной к постоянному напряжению, равен нулю, так как конденсатор, зарядившись до величины питающего напряжения, размыкает цепь. Следовательно, ток переходного процесса определяется только свободным током. Уравнение свободного тока

Дифференцируя уравнение свободного тока, получаем

тогда характеристическое уравнение

откуда корень характеристического уравнения

Ток переходного процесса

Определяем постоянную интегрирования А. Полагая t=0 и учитывая, что напряжение на емкости скачком возникнуть не может (конденсатор до начала переходного процесса не был заряжен  ), получаем
), получаем

Таким образом, ток переходного процесса будет равен

2. Синусоидальное напряжение. Определяем установившийся ток:



Воспользуемся выражением для свободного тока из предыдущей задачи. Тогда ток переходного процесса

Определяем постоянную интегрирования А:

откуда 
Найдем ток  в момент включения:
в момент включения:
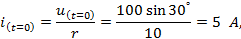
следовательно, 
Таким образом, ток переходного процесса будет равен

Задача 3. Определить емкость C конденсатора в схеме с последовательным соединением резистора и конденсатора, включенной на постоянное напряжение  =200 B, из условия, что через время
=200 B, из условия, что через время  после включения напряжения на конденсаторе при заряде его через резистор с сопротивлением r =5мОм достигнет значения
после включения напряжения на конденсаторе при заряде его через резистор с сопротивлением r =5мОм достигнет значения  =200 B. Найти значение тока
=200 B. Найти значение тока  в момент
в момент  .
.
Решение. Выражение для напряжения на конденсаторе во время переходного процесса в рассматриваемой цепи имеет вид  . Из этого выражения определим значение емкости конденсатора С. При
. Из этого выражения определим значение емкости конденсатора С. При  ,
,  , следовательно
, следовательно  , откуда
, откуда  . Отсюда
. Отсюда 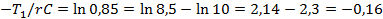 , т.е.
, т.е.  Окончательно
Окончательно

Выражение для тока в цепи запишем в виде

Подставляя в это выражение значения  , найдем
, найдем

Дата добавления: 2015-04-16; просмотров: 277; Мы поможем в написании вашей работы!; Нарушение авторских прав |