Периодические несинусоидальные токи в электрических цепях

После изучения данного раздела студенты должны:

1) знать значение терминов: электрический фильтр, амплитудно-частотный и фазо-частотный спектры, коэффициент пульсации, коэффициент искажения формы кривой; назначение сглаживающего, полосового, заградительного избирательного фильтров;

2) понимать причины возникновения несинусоидальных токов; принцип работы дифференцирующих и интегрирующих цепей; влияние формы кривой тока и напряжения на показания приборов различных систем;

3) уметь анализировать электрическое состояние линейной цепи несинусоидального тока методом суперпозиции, работу простейших фильтров.

При изучении настоящего раздела необходимо усвоить, что источников с абсолютно постоянной или синусоидальной э.д.с. не существует. Различные источники энергии в силу ряда причин создают пульсирующие, медленно меняющиеся или незначительно отличающиеся от синусоидальной формы напряжения.

Причинами появления несинусоидальных токов являются:

1) несовершенство источников постоянной и синусоидальной э.д.с.;

2) подключение к линейной цепи генераторов, создающих специальную форму напряжения;

3) наличие различного рода нелинейных элементов в электрической цепи.

При расчете цепей, находящихся под воздействием периодических несинусоидальных величин, необходимо знать способы их представления:

1) графики зависимости мгновенных значений несинусоидальных токов и напряжений от времени;

2) аналитический способ разложения периодических функций в ряд Фурье, из которого для практических целей берут ограниченное число первых членов ряда. В разложении в ряд Фурье в общем случае представлены постоянная составляющая, основная (первая) гармоническая составляющая, имеющая период, равный периоду данного несинусоидального воздействия, высшие гармонические составляющие и их начальные фазы. Основную и высшие гармонические составляющие обычно называют гармониками. Амплитуды и начальные фазы гармоник определяют спектральный состав несинусоидальной кривой, который может быть представлен в виде диаграмм амплитудно-частотного и фазо-частотного спектров.

При анализе электрических цепей с несинусоидальными напряжениями и токами частот имеют дело с действующими значениями этих величин:

Таким образом, действующее значение несинусоидального напряжения или тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник несинусоидального напряжения или тока.

Действующее значение каждой гармоники

Среднее значение мощности при несинусоидальных напряжениях и токе равно сумме средних значений мощностей от постоянных составляющих и каждой гармоники тока и напряжения:

Форму периодических несинусоидальных кривых принято характеризовать некоторыми коэффициентами: амплитуды , формы , искажения 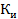и др. Разложение в ряд Фурье позволяет заменить на основании принципа суперпозиции реальный источник несинусоидального напряжения совокупностью последовательно включенных источников.

Таким образом, мгновенные значения искомых токов и напряжений определяют путем суммирования найденных в результате расчета постоянных и гармонических составляющих тока или напряжения. При расчете цепей следует учитывать, что сопротивления емкостного и индуктивного элементов зависят от частоты: сопротивление индуктивного элемента возрастает с увеличением номера k гармоники, т.е. , а сопротивление емкостного элемента уменьшается с увеличением порядкового номера гармоники, т.е. . В тех случаях, когда это требуется по условиям работы электрических цепей для изменения формы кривой тока или напряжения, применяются специальные устройства, содержащие индуктивные катушки и конденсаторы. Эти устройства называются электрическими фильтрами.

Задача 1.Для кривой напряжения однополупериодного выпрямления

(рис.23). Найти действующее значение напряжения путем непосредственного интегрирования. Сравнить найденный результат с расчетом по гармоникам ряда Фурье, учитывая только: а) первый член ряда, б) первые три члена ряда. Оценить погрешность 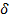в процентах. Определить коэффициенты , , .

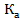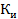Разложение в ряд Фурье:

Решение. Находим действующее и среднее значения напряжения непосредственным интегрированием:

Учитывая только первый член разложения в ряд Фурье, оценим погрешность :

С учетом трех членов разложения получим

Получаем погрешность, вполне допустимую при инженерных расчетах. Таким образом, остальными членами разложения в ряд Фурье можно пренебречь.

Определим коэффициенты, характеризующие форму кривой напряжения:

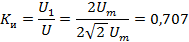
Задача 2. Определить индуктивность резонансного фильтра (рис.24), являющегося бесконечно большим сопротивлением для тока первой гармоники и не представляющего сопротивления для тока седьмой гармоники. Дано:

Решение. Чтобы исключить первую гармонику в нагрузке, необходимо выполнить условие резонанса токов:

отсюда

Чтобы выделить седьмую гармонику в нагрузке следует обеспечить условие резонанса напряжений для седьмой гармоники:

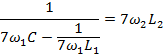
отсюда

Задача 3. Найти показания приборов электромагнитной системы (рис.25), записать для мгновенных значений всех токов и определить их коэффициенты искажения.

Дано:

Решение. Находим токи в ветвях от первой гармоники:

,

где

Определяем токи в ветвях от третьей гармоники:

На третьей гармонике в параллельном контуре резонанс токов

,

где

Показание приборов будут иметь следующие значения:

Мгновенные значения токов имеют вид:

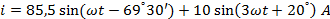
Коэффициенты искажения токов:

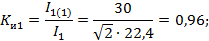
Наиболее искажена кривая тока на емкостном элементе.