Расчеты интенсивности отказов и вероятности безотказной работы в системах электроснабжения.

Для расчета показателей надежности используются модели отказов и модели надежности. Модели отказов применяются для невосстанавливаемых элементов. В этом случае поток отказов считается простейшим, параметр потока отказов равен интенсивности отказов, а вероятность безотказной работы описывается экспоненциальным законом.

P(t) = e^{– λt}; Q(t) = 1 – e^{– λt}; φ(t) = λe^{– λt}; λ(t) = λ = const; ω(t) = λ.

Модели надежности применяются для восстанавливаемых элементов. В этом случае поток событий состоит из двух процессов – отказов, характеризующихся параметром потока отказов ω(t), и восстановлений, характеризующихся интенсивностью восстановлений μ(t). Предполагая оба потока простейшими, можно установить связь между параметрами:

ω = 1/ , где – средняя наработка на отказ;

μ = 1/ , где – среднее время восстановления функционирования.

Вероятности в этом случае определяются по формулам:

; . ; .

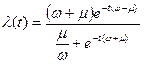При отсутствии восстановления (μ = 0) λ(t) = ω и закон распределения вероятностей становится экспоненциальным.

При t →∞ – коэффициент готовности.

Для расчетов надежности систем с пуассоновским потоком отказов можно воспользоваться распределением Пуассона вероятности возникновения m отказов за время t:

, где 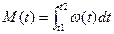– мат.ожидание числа отказов в интервале времени (t₁, t₂).

Для систем с λ = const M(t) = λt: .

Если доля внезапных отказов невелика, т.е. система работает в благоприятных условиях, используется нормальный закон распределения. Вероятность безотказной работы при этом рассчитывается по формуле:

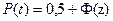, где , σ – среднеквадратическое отклонение времени наработки на отказ;

– интегральная функция Лапласа.

Вероятность того, что средняя наработка на отказ находится в интервале времени (t₁, t₂)

.

При последовательном соединении элементов системы вероятности отказа складываются, а вероятности безотказной работы перемножаются. При экспоненциальном законе распределения вероятность отказа системы из последовательно соединенных элементов также подчиняется экспоненциальному закону.

P_Σ(t) = P₁(t)P₂(t)…P_n(t); Q_Σ(t) = Q₁(t)+Q₂(t)+…+Q_n(t); λ_Σ = λ₁+λ₂+…+ λ_n.